Answer
Verified461.1k+ views
Hint: It is better to understand that a quadrilateral is a four sided polygon in geometry. Think about what form can a quadrilateral take if all the angles of the quadrilateral are equal.
Complete step-by-step answer:
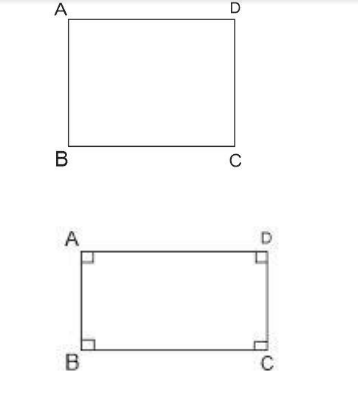
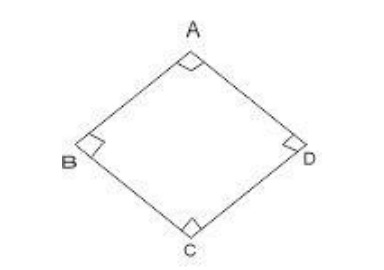
It is given in the question that the four angles of a quadrilateral are equal.
Sum of all the angles of a quadrilateral is equal to ${360^0}$
Let $\angle A,\angle B,\angle C,\angle D$ be the four angles of the Quadrilateral $ABCD$.
Since, the Sum of the angles of quadrilateral $ = {360^0}$
Therefore $\angle A + \angle B + \angle C + \angle D = {360^0}$ . . . (1)
But all the angles are equal in measure
$ \Rightarrow \angle A = \angle B = \angle C = \angle D$
Therefore, we can write equation (1) in terms of any one angle.
$ \Rightarrow \angle A + \angle A + \angle A + \angle A = {360^0}$
$ \Rightarrow 4\angle A = {360^0}$
Dividing both the sides by 4 we get
$\angle A = \dfrac{{{{360}^0}}}{4}$
$ \Rightarrow \angle A = {90^0}$
Therefore, each angle of the quadrilateral $ = {90^0}$
Therefore, It must be a square or a rectangle as only squares and rectangles have every angle equal to ${90^0}$
Note: You cannot solve a question like this if you don’t know what a quadrilateral is. If you don’t know the sum of all the angles of a quadrilateral. And you won’t be able to tell which shape will it take if you don’t know the properties of commonly used figures like rectangle, square, parallelogram etc. Knowing basic properties of standard geometrical shapes is important.
Complete step-by-step answer:
It is given in the question that the four angles of a quadrilateral are equal.
Sum of all the angles of a quadrilateral is equal to ${360^0}$
Let $\angle A,\angle B,\angle C,\angle D$ be the four angles of the Quadrilateral $ABCD$.
Since, the Sum of the angles of quadrilateral $ = {360^0}$
Therefore $\angle A + \angle B + \angle C + \angle D = {360^0}$ . . . (1)
But all the angles are equal in measure
$ \Rightarrow \angle A = \angle B = \angle C = \angle D$
Therefore, we can write equation (1) in terms of any one angle.
$ \Rightarrow \angle A + \angle A + \angle A + \angle A = {360^0}$
$ \Rightarrow 4\angle A = {360^0}$
Dividing both the sides by 4 we get
$\angle A = \dfrac{{{{360}^0}}}{4}$
$ \Rightarrow \angle A = {90^0}$
Therefore, each angle of the quadrilateral $ = {90^0}$
Therefore, It must be a square or a rectangle as only squares and rectangles have every angle equal to ${90^0}$
Note: You cannot solve a question like this if you don’t know what a quadrilateral is. If you don’t know the sum of all the angles of a quadrilateral. And you won’t be able to tell which shape will it take if you don’t know the properties of commonly used figures like rectangle, square, parallelogram etc. Knowing basic properties of standard geometrical shapes is important.