Question

The frequency of a second’s pendulum is:
A. 0.5Hz
B. 1.0Hz
C. 2.0Hz
D. 5.5Hz

Answer 1

Hint: Recall that the frequency is the reciprocal of time period. In other words, frequency is the number of oscillations per second. Firstly, you should think of the particularity of a second’s pendulum, which will lead you to its time period, and its reciprocal will give you the final answer.

Formula used:
$f=\dfrac{1}{T}$

Complete step-by-step answer:
We are well acquainted with simple pendulums. Simple pendulum consists of a body of mass (typically a bob of mass m) suspended from a pivot on a frictionless string and is free to carry out oscillation about two maximas at two ends. So, what is the physics behind it?
When a pendulum gets displaced from its equilibrium position, gravity comes into action as the restoring force that pulls it back towards the equilibrium position. This gravity along with the mass of the pendulum however results in to and fro oscillation of the pendulum about its equilibrium point.

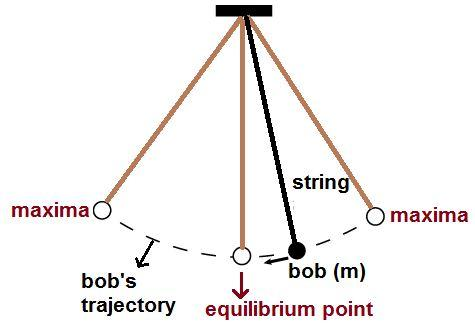
Let us now define one complete oscillation. If we were to release the bob from the maxima at the right end, its swing from the right-end maxima to the left-end maxima and back is said to be one complete oscillation. The time taken by the bob to complete one oscillation is what we call its time period.
Frequency, by definition, is the number of oscillations per unit time. We can represent it by, ‘f’ and its unit is Hz or ${{s}^{-1}}$ .
Also, it is the reciprocal of time period (represented by ‘T’). That is,
$f=\dfrac{1}{T}$ ……………….. (1)
In the given question, we are asked about second’s pendulum. Second’s pendulum is that pendulum whose time period is 2s. In other words, a second’s pendulum takes 2 seconds in order to complete one full oscillation. So, the pendulum takes 1 second to swing from right maxima to the left maxima and another second to swing back. So, that makes 2 seconds in total.
So for a second’s pendulum, time period (T) is,
$T=2s$ ……………… (2)
Substituting (2) in (1) we get the frequency of a second’s pendulum as,
$f=\dfrac{1}{T}=\dfrac{1}{2}$
$f=0.5Hz$
So, the correct answer is “Option A”.

Note: Though the name indicates the time period of a second’s pendulum to be 1s, its time period really is 2s. Also, we are asked to find the frequency, that is, the number of oscillations in 1s. If it takes 2 seconds to complete one full oscillation, then obviously at the end of one second, half the oscillation is completed and hence the answer.