Question

The fundamental frequency of an open pipe is 30 Hz. If one end of the pipe is closed then the fundamental frequency will be
A. 15 Hz
B. 30 Hz
C. 45 Hz
D. 60 Hz

Answer 1

Hint: When the open pipe is closed from one end, it acts as a closed pipe. Use the formula of fundamental frequency for an open pipe and closed pipe, and establish two equations. Take the ratio of these equations to then find the value of the fundamental frequency of the closed pipe by substitution of value of open pipe frequency.

Formula Used:
The fundamental frequency of open pipe, ${v_ \circ } = \dfrac{{\text{v}}}{{2L}}$
The fundamental frequency of closed pipe, ${v_ \circ ^{'}} = \dfrac{{\text{v}}}{{4L}}$
where v represents the speed of sound and L represents the length of the pipe.

Complete step-by-step answer:
Standing waves are a combination of two stationary waves such that these two waves are moving in the opposite direction having sample frequency and amplitude and when superimposed on each other their energies are either canceled out or added together.
When a pipe is open at both ends having length L, then the standing wave produced in it has two antinodes also known as pressure nodes at both ends. This is known as the first harmonic or the fundamental harmonic.

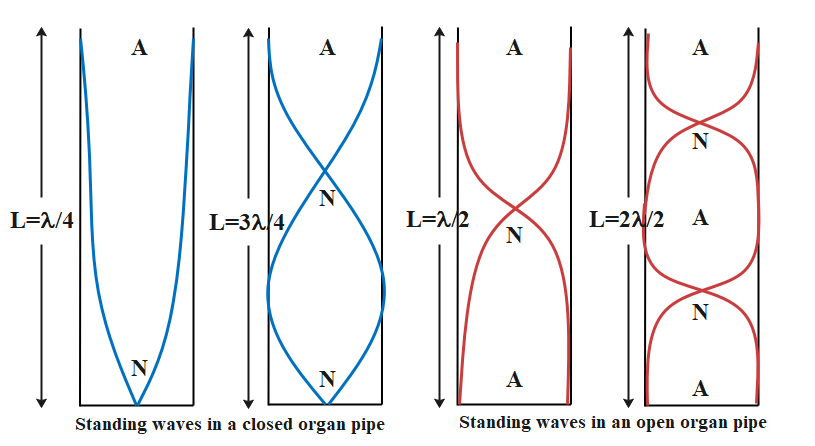
The pipe of length L is initially open at both ends, in this case, let sound’s frequency be ${v_ \circ }$ and v the speed of sound${v_ \circ }$
So, we have: ${v_ \circ } = \dfrac{{\text{v}}}{{2L}} \cdots \cdots \cdots \cdots \left( 1 \right)$
This corresponds to the fundamental frequency of the open pipe.
When the pipe is closed at one end, it becomes a closed pipe. And the fundamental frequency for the closed pipe is given by:
${v_ \circ ^{'}} = \dfrac{{\text{v}}}{{4L}} \cdots \cdots \cdots \cdots \left( 2 \right)$
Given:
The fundamental frequency of open pipe, ${v_ \circ } = 30$
Taking ratio of equation (1) and (2):
$\eqalign{
  & \dfrac{{v_ \circ ^{'}}}{{{v_ \circ }}} = \dfrac{{\text{v}}}{{4L}} \times \dfrac{{2L}}{{\text{v}}} \cr
  & \Rightarrow \dfrac{{v_ \circ ^{'}}}{{{v_ \circ }}} = \dfrac{1}{2} \cr
  & \Rightarrow {v_ \circ ^{'}} = \dfrac{{{v_ \circ }}}{2} \cr
  & \Rightarrow {v_ \circ ^{'}} = \dfrac{{30}}{2}{\text{ }}\left[ {\because {v_ \circ } = 30\left( {given} \right)} \right] \cr
  & \therefore {v_ \circ ^{'}} = 15 \cr} $
Therefore, the correct option is A i.e., 15 Hz.

Note: There are no missing harmonics in an open organ pipe. The quality of sound from an open organ pipe is, therefore, richer than that from a closed organ pipe in which all the even harmonics of the fundamentals are missing.