Question

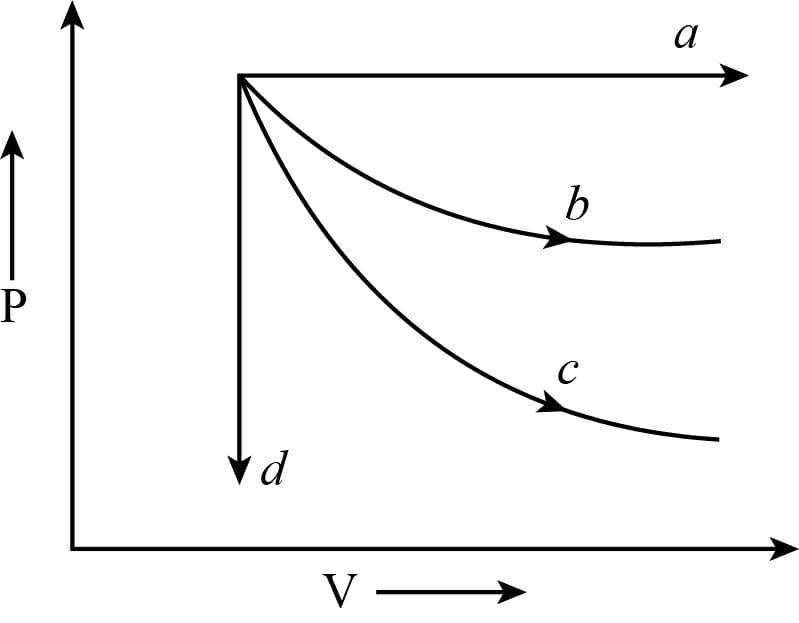
The given diagram shows four processes, i.e. isochoric, isobaric, isothermal, and adiabatic the correct assignment of process, in the same order given by

Answer 1

Hint: As we all know about the isothermal process which occurs at a constant temperature. Isochoric process which occurs at constant volume. Isobaric process which occurs at constant pressure. We are familiar with the adiabatic process in which no heat between the system and surrounding.

Complete Step-by-step Solution
Given: As we can see that the diagram shows four processes, i.e. isochoric, isobaric, isothermal, and adiabatic the correct assignment of process, in the same order given by
Here, we can notice the graph shows the isochoric process because the pressure will be decreased, keeping the volume constant. It means $V =$ constant, $dV = 0$.
We can see that also, the graph ‘$a$’ shows the isobaric process because volume increases, keeping the temperature and pressure constant. In this case, $dP = 0$
The curve ‘$b$’ shows the isothermal process in which pressure and volume changes and temperature remain constant i.e. $dT = 0$.
And the curve ‘$c$’ shows the adiabatic process in which the pressure, temperature, and volume are changed but there is no exchange of heat between the system and surroundings.
The slope of the adiabatic process will be more than the isothermal process so; ‘$b$’ shows the isothermal process and ‘$c$’ indicate the adiabatic process.

The correct assignment of process, in the same order given by (from the graph) d, a, b, c.

Additional information:
So thereby we can conclude that the above statement of the processes can be identified with this equation.
${\rm{P}}{{\rm{V}}^n} = {\rm{constant}}{\rm{.}}$ (This is a polytropic process)
A polytropic process is a generalized process. For this polytropic process, we need no assumptions; the gas can be real or ideal and it is an equation for an arbitrary process.
If $n = 0$ then $P $= constant (isobaric process) which is represented by $a$.
If $n = 1$ then $PV$ = constant (isothermal process) which is represented by $b$.
If $n = \gamma $ then $PV_{\gamma}$ = constant (adiabatic process) which is represented by $c$.
Here $\gamma $ is the ratio of specific heats.
At last $n = \infty $ , then V = constant. (Isochoric process) which is represented by $d$.

Note:
In an adiabatic process, compression and expansion should occur suddenly; so that heat does not get time to be exchanged with surroundings, so the adiabatic process has more slope than the isothermal process, on the other hand, the isothermal process has to be very slow to maintain the temperature equilibrium with the surroundings.