Question

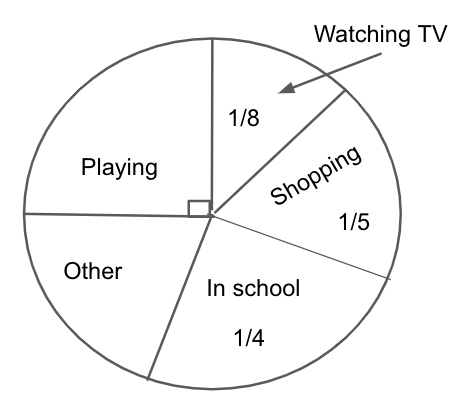
The given pie chart shows how Prabhat spent his time on a certain day.
a) How much time did he spend in playing?
b) How much time did he spend in school?
c) How much time did he spend in other activities?

Answer 1

Hint: Consider that the total time in a day is 24 hours and total circle has a probability 1. So, first we will compute the time spend by him in different activities by multiplying probability of the particular activity by 24 hours. Then we will use the find the time spend by him in the other activities from the given pie chart using the formula,\[{\text{Other}} = {\text{Total circle}} - \left( {{\text{Playing}} + {\text{Watching TV}} + {\text{Sleeping}} + {\text{In School}}} \right)\] for the third part.

Complete step by step answer:

We know that the total time in a day is 24 hours.
We are given that the probability of Prabhat spends while watching TV is \[\dfrac{1}{8}\], shopping is \[\dfrac{1}{5}\], in school is \[\dfrac{1}{4}\] from the given figure.
Since the region for playing covers the 90 degrees, the probability Prabhat spends while playing is \[\dfrac{1}{4}\].

(i) We are given that Prabhat spends \[\dfrac{1}{4}th\] of a circle in playing from the given pie chart.

We will now find the time spent by him playing in a day.

\[ \Rightarrow \dfrac{1}{4} \times 24 = 6{\text{ hours}}\]

Hence, time spent by him in playing is 6 hours.

(ii) We are given that Prabhat spends \[\dfrac{1}{4}th\] of a circle in school from the given pie chart.

We will now find the time spend by him in school in a day by multiplying the probability of playing with 24, we get

\[ \Rightarrow \dfrac{1}{4} \times 24 = 6{\text{ hours}}\]

Hence, the time spent by him in school is 6 hours.

(iii) We know that the sum of all the probabilities of the circle is 1.

We will now find the time spend by him in the other activities from the given pie chart using the formula,
\[{\text{Other}} = {\text{Total circle}} - \left( {{\text{Playing}} + {\text{Watching TV}} + {\text{Sleeping}} + {\text{In School}}} \right)\].

Using the probabilities of the time spent by Prabhat in school, playing, watching TV and sleeping in the above formula, we get

\[
   \Rightarrow {\text{Other}} = 1 - \left( {\dfrac{1}{4} + \dfrac{1}{8} + \dfrac{1}{5} + \dfrac{1}{4}} \right) \\
   \Rightarrow {\text{Other}} = 1 - \left( {\dfrac{{10 + 5 + 8 + 10}}{{40}}} \right) \\
   \Rightarrow {\text{Other}} = 1 - \dfrac{{33}}{{40}} \\
   \Rightarrow {\text{Other}} = \dfrac{{40 - 33}}{{40}} \\
   \Rightarrow {\text{Other}} = \dfrac{7}{{40}} \\
 \]

Thus, Prabhat spends \[\dfrac{7}{{40}}th\] of a circle in other activities.

We will now find the time spend by him in other activities in a day.

\[ \Rightarrow \dfrac{7}{{40}} \times 24 = 4.2{\text{ hours}}\]

Hence, the time spends by him in other activities is \[4.2\] hours.

Note: In solving these types of questions, students should first carefully read the question and the pie chart. One should know that the probability is simply how likely something is to happen. Some students take the time as 1 day, which is wrong. So we must know that the total time in a day is 24 hours and the total circle has a probability of 1. When we have written that Prabhat spends the time in a circle, it means we have to evaluate the product of the probability of the particular activity and 24 hours to find the time spend by him.