
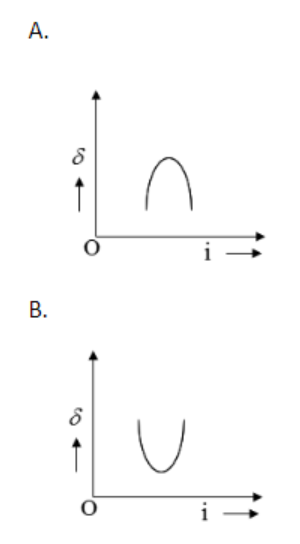
The graph between angle of deviation and angle of incidence (i) for a triangular prism is represented by:


Answer
510.9k+ views
1 likes
Hint: We can solve this problem with the help of a refraction diagram through the prism. We can find the relation between the angle of deviation and angle of incidence. From this, we can find out the graphical representation of the angle of deviation and angle of incidence.
Complete step by step answer:
A prism is a wedge-shaped portion of a transparent refracting medium bounded by two plane faces inclined to each other at a certain angle. Triangle ABC represents the principle section of the prism. When a ray of light enters from lighter medium to denser medium it bends towards the normal. Here the air is lighter medium and prism is denser medium. As the ray moves out of the prism it again undergoes refraction on moving from denser medium to lighter medium. This time, the refracted ray bends away from the normal.
The angle of deviation
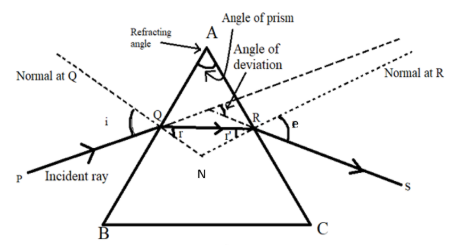
From the quadrilateral AQNR, the angle Q and R are right angles. Therefore, the sum of the remaining angles of the quadrilateral will be
From the triangle QNR, we can say that,
We can compare these two equations. So, we will get,
The total deviation
Hence, we can write this equation as,
From this equation, we can say that the angle of deviation depends on the angle of incidence. According to this formula, the plot between the angle of deviation and angle of incidence will be like this.
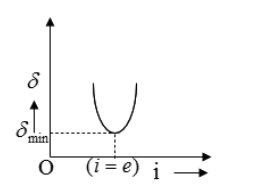
When the angle of incidence and angle of emergence are equal, then the angle of deviation will be minimum. Thus, it can be called a minimum deviation.
According to the graph, we can say that the correct answer is option B.
Note: The deviation produced by the prism is maximum when either the angle of incidence or angle of emergence is
For any other angle of deviations except the angle of minimum deviation, the angle of incidence and angle of emergence can’t be interchanged. That means it has specific values. From the relation between the angle of incidence and angle of deviation, we can say that it is not a linear relationship. So, we can avoid other options.
Complete step by step answer:
A prism is a wedge-shaped portion of a transparent refracting medium bounded by two plane faces inclined to each other at a certain angle. Triangle ABC represents the principle section of the prism. When a ray of light enters from lighter medium to denser medium it bends towards the normal. Here the air is lighter medium and prism is denser medium. As the ray moves out of the prism it again undergoes refraction on moving from denser medium to lighter medium. This time, the refracted ray bends away from the normal.
The angle of deviation

From the quadrilateral AQNR, the angle Q and R are right angles. Therefore, the sum of the remaining angles of the quadrilateral will be
From the triangle QNR, we can say that,
We can compare these two equations. So, we will get,
The total deviation
Hence, we can write this equation as,
From this equation, we can say that the angle of deviation depends on the angle of incidence. According to this formula, the plot between the angle of deviation and angle of incidence will be like this.

When the angle of incidence and angle of emergence are equal, then the angle of deviation will be minimum. Thus, it can be called a minimum deviation.
According to the graph, we can say that the correct answer is option B.
Note: The deviation produced by the prism is maximum when either the angle of incidence or angle of emergence is
For any other angle of deviations except the angle of minimum deviation, the angle of incidence and angle of emergence can’t be interchanged. That means it has specific values. From the relation between the angle of incidence and angle of deviation, we can say that it is not a linear relationship. So, we can avoid other options.
Latest Vedantu courses for you
Grade 10 | MAHARASHTRABOARD | SCHOOL | English
Vedantu 10 Maharashtra Pro Lite (2025-26)
School Full course for MAHARASHTRABOARD students
₹33,300 per year
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

What are the major means of transport Explain each class 12 social science CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE




