Question

The graph of an identity function is
[a] A straight line parallel to the x-axis
[b] A straight line parallel to the y-axis
[c] A straight line passing through the origin
[d] None of the above

Answer 1

Hint: Use the fact that the identity function maps every value in the domain to itself in the codomain. Hence if y=f(x) is an identity function, then y = x. Use the fact that the equation of form y = mx+c is of a straight line of slope m and x-intercept c. Hence draw the graph of the identity function and verify which of the options is correct.

Complete step-by-step answer:
We know that the identity function on the set of a real number is a relation from $\mathbb{R}$ to $\mathbb{R}$ such that $I=\left\{ \left( x,x \right),x\in \mathbb{R} \right\}$
Hence, if we have y=f(x) is an identity relation, then $\left( x,y \right)\in \left\{ \left( x,x \right),x\in \mathbb{R} \right\}$
Hence, we have
y =x
Hence the identity function is the function y =x.
Now, we know that the curve y = mx+c represents a straight line with slope m and x-intercept c.
Hence the identity function is a straight line with slope 1 and x-intercept 0.
Hence the graph of the identity function is as follows

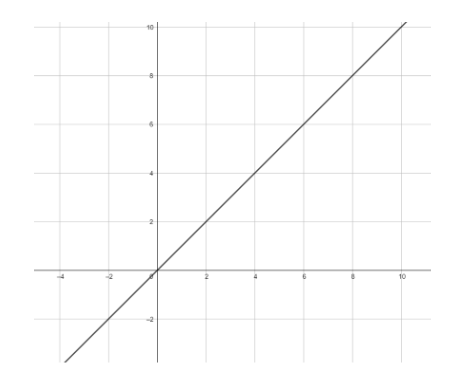
Since the graph is not parallel to the x-axis, option [a] is incorrect
Since the graph is not parallel to the y-axis, option [b] is incorrect.
Since the graph passes through (0,0) and is a straight line, option [c] is correct.
Hence option [c] is the only correct answer.

Note: In these types of questions, we need to know the basic definitions of various functions and the general equations of various types of curves.