
The graph of current versus time in a wire is given by
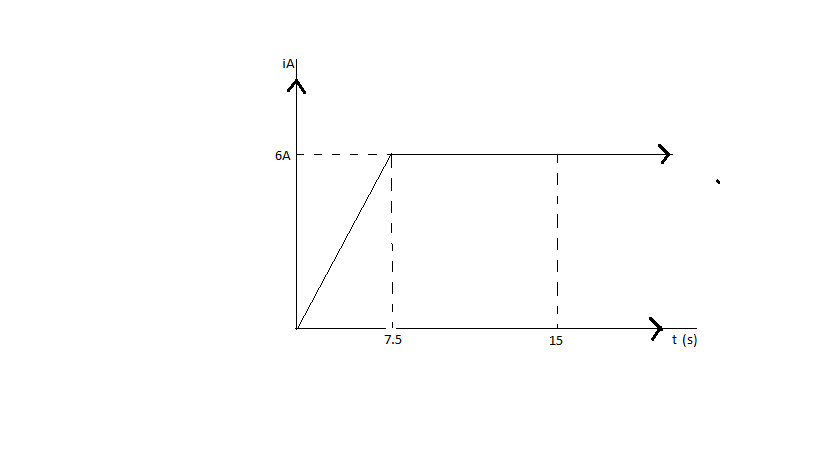
If charge flows through the wire in $7.5s$ is ${q_1}$ and that flows through the wire in $15s$ is ${q_2}$, then ratio ${q_1}:{q_2}$ is
A. $2:1$
B. $1:2$
C. $4:1$
D. $1:4$
E. $1:3$
Answer
140.7k+ views
Hint: From the graph it is evident that the current remains the same in both the time stamps. So we can just use the current formula to calculate the charges in both the cases and then divide them to obtain the ratio.
Formulas used
$i = \dfrac{q}{t}$ where $i$ is the current flowing through the conductor, $q$ is the charge and $t$ is the time taken.
Complete step by step answer
Electric current is defined as the flow of electric charge (electrons) per unit time through a conducting medium. Its SI unit is Ampere and is symbolized by $A$. It is measured using a device called the ammeter.
The flow of electric current is due to the stream of charged particles such as electrons from a region of higher potential to a region of lower potential. This means that current can only flow through a medium when there is a potential difference present.
Now, we can solve the question given by using the definition of current which gives us the relation,
$i = \dfrac{q}{t}$ where $i$ is the current flowing through the conductor, $q$ is the charge and $t$ is the time taken.
On the graph given above we see that the value of current is constant from time $t = 7.5s$to $15s$ and beyond.
So, using the current equation we can write,
${q_1} = 6 \times 7.5$$C$ where ${q_1}$is the charge at $t = 7.5s$
Similarly,
${q_2} = 6 \times 15C$ where ${q_2}$ is the charge at $t = 15s$
Dividing these two equations we get,
$\dfrac{{{q_1}}}{{{q_2}}} = \dfrac{{6 \times 7.5}}{{6 \times 15}}$
$ \Rightarrow \dfrac{{{q_1}}}{{{q_2}}} = \dfrac{1}{2}$
${q_1}:{q_2} = 1:2$
Therefore, the correct option is B.
Note: In a conductor, the total current is due to the flow of electrons which are negative charge carriers. However, in case of semiconductors, the flow of current is due to both positive and negative carriers. Unlike conductors, semiconductors can only conduct electricity at very high temperatures. This is due to the fact that semiconductors have a negative coefficient of resistance with temperature. Which means that their resistance decreases with increase in temperature.
Formulas used
$i = \dfrac{q}{t}$ where $i$ is the current flowing through the conductor, $q$ is the charge and $t$ is the time taken.
Complete step by step answer
Electric current is defined as the flow of electric charge (electrons) per unit time through a conducting medium. Its SI unit is Ampere and is symbolized by $A$. It is measured using a device called the ammeter.
The flow of electric current is due to the stream of charged particles such as electrons from a region of higher potential to a region of lower potential. This means that current can only flow through a medium when there is a potential difference present.
Now, we can solve the question given by using the definition of current which gives us the relation,
$i = \dfrac{q}{t}$ where $i$ is the current flowing through the conductor, $q$ is the charge and $t$ is the time taken.
On the graph given above we see that the value of current is constant from time $t = 7.5s$to $15s$ and beyond.
So, using the current equation we can write,
${q_1} = 6 \times 7.5$$C$ where ${q_1}$is the charge at $t = 7.5s$
Similarly,
${q_2} = 6 \times 15C$ where ${q_2}$ is the charge at $t = 15s$
Dividing these two equations we get,
$\dfrac{{{q_1}}}{{{q_2}}} = \dfrac{{6 \times 7.5}}{{6 \times 15}}$
$ \Rightarrow \dfrac{{{q_1}}}{{{q_2}}} = \dfrac{1}{2}$
${q_1}:{q_2} = 1:2$
Therefore, the correct option is B.
Note: In a conductor, the total current is due to the flow of electrons which are negative charge carriers. However, in case of semiconductors, the flow of current is due to both positive and negative carriers. Unlike conductors, semiconductors can only conduct electricity at very high temperatures. This is due to the fact that semiconductors have a negative coefficient of resistance with temperature. Which means that their resistance decreases with increase in temperature.
Recently Updated Pages
Young's Double Slit Experiment Step by Step Derivation

Difference Between Circuit Switching and Packet Switching

Difference Between Mass and Weight

JEE Main Participating Colleges 2024 - A Complete List of Top Colleges

JEE Main Maths Paper Pattern 2025 – Marking, Sections & Tips

Sign up for JEE Main 2025 Live Classes - Vedantu

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

JEE Main 2025: Derivation of Equation of Trajectory in Physics

A point charge + 20mu C is at a distance 6cm directly class 12 physics JEE_Main

JEE Main Exam Marking Scheme: Detailed Breakdown of Marks and Negative Marking

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

Electric Field Due to Uniformly Charged Ring for JEE Main 2025 - Formula and Derivation

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Electric field due to uniformly charged sphere class 12 physics JEE_Main

JEE Main 2025: Conversion of Galvanometer Into Ammeter And Voltmeter in Physics

Degree of Dissociation and Its Formula With Solved Example for JEE

Dual Nature of Radiation and Matter Class 12 Notes: CBSE Physics Chapter 11

Formula for number of images formed by two plane mirrors class 12 physics JEE_Main




