
The graph of the equation of the form \[y = mx\] is a line which always passes through
A. \[\left( {0,m} \right)\]
B. \[\left( {x,0} \right)\]
C. \[\left( {0,y} \right)\]
D. \[\left( {0,0} \right)\]
Answer
578.4k+ views
Hint: We will first consider the graph of the general form of equation, \[y = mx\]. As we need to find the point through which the line passes, so we will make the graph of the line \[y = mx\] and from there we can check through which point the line is passing by. As we know that the graph of a linear equation is always a straight line and the given equation is also a linear equation then the graph we have will also be of the straight line.
Complete step by step Answer:
As we will first consider the given equation of a line in the question, that is \[y = mx\].
We will first make the graph of the line \[y = mx\] where \[m\] represents the slope of the line.
Thus, we get,
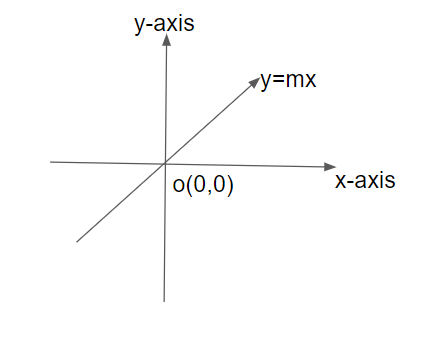
Now, the graph is of a straight line and from the graph we can see that the line \[y = mx\] is passing through the origin \[{\text{o}}\left( {0,0} \right)\].
Thus, we can conclude that the equation \[y = mx\] always passes through the origin.
Hence, option D is correct.
Note: As the graph of the linear equation is always a straight line so we also have a linear equation whose graph is of a straight line. Also, every point on the straight line is the solution of the linear equation, and as we can observe that the line is passing through the origin. The general form of the equation with slope \[m\] is \[y - {y_1} = m\left( {x - {x_1}} \right)\]. Also, while constructing the figure, draw the line of the equation properly for solving the further solution.
Complete step by step Answer:
As we will first consider the given equation of a line in the question, that is \[y = mx\].
We will first make the graph of the line \[y = mx\] where \[m\] represents the slope of the line.
Thus, we get,
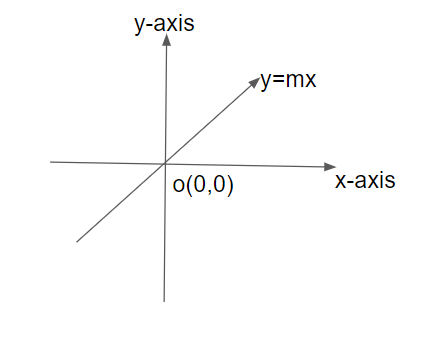
Now, the graph is of a straight line and from the graph we can see that the line \[y = mx\] is passing through the origin \[{\text{o}}\left( {0,0} \right)\].
Thus, we can conclude that the equation \[y = mx\] always passes through the origin.
Hence, option D is correct.
Note: As the graph of the linear equation is always a straight line so we also have a linear equation whose graph is of a straight line. Also, every point on the straight line is the solution of the linear equation, and as we can observe that the line is passing through the origin. The general form of the equation with slope \[m\] is \[y - {y_1} = m\left( {x - {x_1}} \right)\]. Also, while constructing the figure, draw the line of the equation properly for solving the further solution.
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 English: Engaging Questions & Answers for Success

Master Class 11 Chemistry: Engaging Questions & Answers for Success

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE

Summary of the poem Where the Mind is Without Fear class 8 english CBSE

What are gulf countries and why they are called Gulf class 8 social science CBSE




