Answer
Verified401.4k+ views
Hint: Here in this question, we have to find the quadrants which graph of the given equation lies, given the value of equation \[xy\] is $k$ which is less than zero means $k$ is the negative value so we have to check the quadrants in the graph weather one of the $x$ or $y$ value will be negative.
Complete step by step solution:
A quadrant is one of the four sections on a Cartesian plane. Each quadrant includes a combination of positive and negative values for $x$ and $y$.
There are four graph quadrants that make up the Cartesian plane. Each graph quadrant has a distinct combination of positive and negative values.
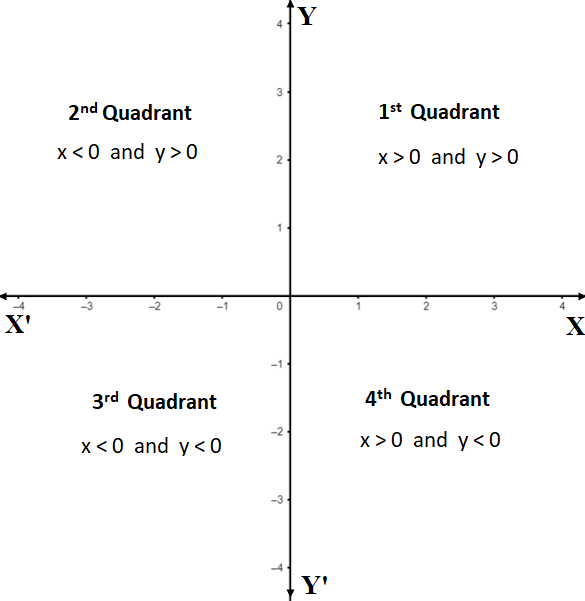
Quadrant I: The first quadrant is in the upper right-hand corner of the plane. Both x and y have positive values in this quadrant.
Quadrant II: The second quadrant is in the upper left-hand corner of the plane. X has negative values in this quadrant and y has positive values.
Quadrant III: The third quadrant is in the bottom left corner. Both x and y have negative values in this quadrant.
Quadrant IV: The fourth quadrant is in the bottom right corner. X has positive values in this quadrant and y has negative values.
Consider the given question
The given equation of graph is
\[ \Rightarrow \,\,xy = k\], where \[k < 0\]
If the value \[k < 0\] (k will be the negative values), then “X” and “Y” must have different signs one of the values ‘X’ and ‘Y’ is negative.
The possible cases are:
\[x > 0\] and \[y < 0\], which is lies in \[IV\] quadrant
\[x < 0\] and \[y > 0\], which lie in \[II\] quadrant.
Hence, the graph of the equation \[xy = k\], where \[k < 0\] lies in \[II\] and \[IV\].
Therefore, option (D) is correct.
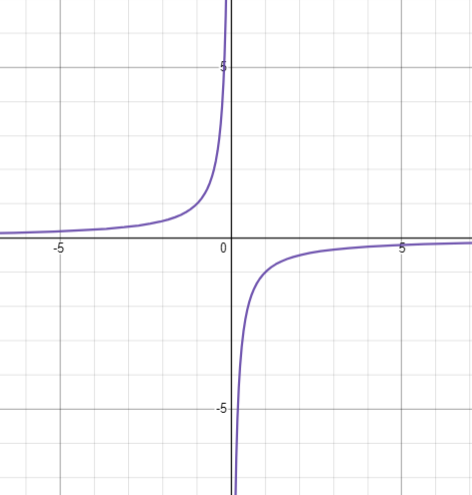
Example of the graph $xy=-1$ which lies in the second and the fourth quadrants.
Note:
A graph quadrant is one of four sections on a Cartesian plane. Each of the four sections has a specific combination of negative and positive values for $x$ and $y$. We plot an ordered pair on graph quadrants. Ordered pairs have $x$ and $y$ values. $x$ is the first value in an ordered pair; $y$ is the second, the $x$ value refers to the pair’s horizontal position on the graph. The $y$ value refers to the vertical position.
Complete step by step solution:
A quadrant is one of the four sections on a Cartesian plane. Each quadrant includes a combination of positive and negative values for $x$ and $y$.
There are four graph quadrants that make up the Cartesian plane. Each graph quadrant has a distinct combination of positive and negative values.
Quadrant I: The first quadrant is in the upper right-hand corner of the plane. Both x and y have positive values in this quadrant.
Quadrant II: The second quadrant is in the upper left-hand corner of the plane. X has negative values in this quadrant and y has positive values.
Quadrant III: The third quadrant is in the bottom left corner. Both x and y have negative values in this quadrant.
Quadrant IV: The fourth quadrant is in the bottom right corner. X has positive values in this quadrant and y has negative values.
Consider the given question
The given equation of graph is
\[ \Rightarrow \,\,xy = k\], where \[k < 0\]
If the value \[k < 0\] (k will be the negative values), then “X” and “Y” must have different signs one of the values ‘X’ and ‘Y’ is negative.
The possible cases are:
\[x > 0\] and \[y < 0\], which is lies in \[IV\] quadrant
\[x < 0\] and \[y > 0\], which lie in \[II\] quadrant.
Hence, the graph of the equation \[xy = k\], where \[k < 0\] lies in \[II\] and \[IV\].
Therefore, option (D) is correct.
Example of the graph $xy=-1$ which lies in the second and the fourth quadrants.
Note:
A graph quadrant is one of four sections on a Cartesian plane. Each of the four sections has a specific combination of negative and positive values for $x$ and $y$. We plot an ordered pair on graph quadrants. Ordered pairs have $x$ and $y$ values. $x$ is the first value in an ordered pair; $y$ is the second, the $x$ value refers to the pair’s horizontal position on the graph. The $y$ value refers to the vertical position.