Question

The height of the hollow cylinder is 12 cm. Find the volume and the surface area of the hollow cylinder if the inner radius is 2cm and the outer radius is 4cm.

Answer 1

Hint: To find the volume and surface area of the hollow cylinder we will simply use the formula to calculate them. Formula to calculate the volume of hollow cylinder is $\pi \left( {{r}_{2}}^{2}-{{r}_{1}}^{2} \right)h$ , where ${{r}_{2}}$ is the outer radius and ${{r}_{1}}$ is the inner radius. Formula to calculate the surface area of the hollow cylinder is $2\pi \left( {{r}_{2}}+{{r}_{1}} \right)h+2\pi \left( {{r}_{2}}^{2}-{{r}_{1}}^{2} \right)$

Complete step-by-step solution:
Since we are given a hollow cylinder whose height is 12cm and the inner radius is 2cm and the outer radius is 4cm.

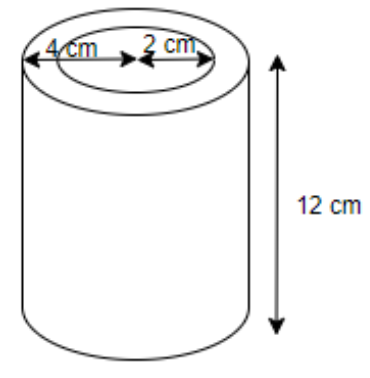
We know that the hollow cylinder is a cylinder which is hollow at the centre. And, if ${{r}_{2}}$ is the outer radius of outer radius of the cylinder, then volume of whole cylinder along with hollow part included is \[\pi {{r}_{2}}^{2}h\] and volume of only hollow part is \[\pi {{r}_{1}}^{2}h\]. So, actual volume of the hollow cylinder is $\pi \left( {{r}_{2}}^{2}-{{r}_{1}}^{2} \right)h$.
So, from the given question we can say that ${{r}_{2}}$ = 4cm and ${{r}_{1}}$ = 2cm.
Hence, volume of the hollow cylinder = $\pi \left( {{4}^{2}}-{{2}^{2}} \right)\times 12c{{m}^{2}}=12\times 12\times \pi c{{m}^{2}}$
So, volume of hollow cylinder = $452.39c{{m}^{2}}$
Now, the total surface area of the hollow cylinder is equal to the summation of the curved surface area of the outer part, curved surface area of the inner part, and area of the ring formed at both the top and bottom of the cylinder.
So, if ${{r}_{2}}$ is the outer radius of outer radius and ${{r}_{1}}$ is the inner radius of the cylinder then, total surface area of the cylinder is $2\pi \left( {{r}_{2}}+{{r}_{1}} \right)h+2\pi \left( {{r}_{2}}^{2}-{{r}_{1}}^{2} \right)$
So, surface area of cylinder whose inner radius ${{r}_{1}}=2cm$ and outer radius ${{r}_{2}}=4cm$ = $2\pi \left( 2+4 \right)\times 12c{{m}^{2}}+2\pi \left( {{4}^{2}}-{{2}^{2}} \right)$
So, surface area of the cylinder = $527.79c{{m}^{2}}$. This is our required solution.

Note: Students are required to not make calculation mistakes while calculating the volume and the surface area and they are also required to memorize the formula of the volume and surface area of the hollow cylinder. Even if students do not remember the formula, they can consider it as two cylinders with a radius of 2 cm and 4 cm. Then, they can compute the volume of each cylinder. Finally, they can subtract the volume of a 2 cm cylinder from that of a 4 cm cylinder. This will not be valid for surface area because the LSA must be added.