Question

The inside perimeter of a running track (shown in figure) is 400m.The length of each of the straight portions is 90m and the ends are semi-circles. If the track is 14m wide everywhere, find the length of the outer track. Also find the area of the track.

Answer 1

Hint: The perimeter of the inside track is 400m. The perimeter includes two straight portions of 90m and the curved length of two semi circles on either side. Find the length of these semi circles by subtracting the lengths of the two straight portions from the total perimeter. With this, we get the radius of the inner semi circles. Now we can find the radius of the outer semi circles by adding the given width to the length of the radius of inner semi circles. The area of the track can be calculated by using the area of ring formula.

Complete step-by-step answer:
Area of the ring is $\pi \left( {{R^2} - {r^2}} \right)$, where R is the radius of the outer circle and r is the radius of the inner circle.
Length of a curved surface (semi circle) is $\pi r$, r is the radius.
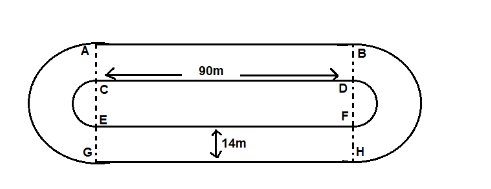
We are given the perimeter of the inside track is 400.
Let r be the radius of the inner circular portion and R is the radius of the outer circular portion and length of the straight portions is l.
Perimeter of the tract includes the length of two straight portions and the lengths of two curved paths (semi circles).
Length of the straight portion is 90m.
Length of the curved path is $\pi r$
$
 {P_i} = l + l + \pi r + \pi r \\
 {P_i} = 400m,l = 90m \\
 \therefore 400 = 90 + 90 + 2\pi r \\
  \to 2\pi r = 400 - 180 \\
  \to 2\pi r = 220 \\
  \to \pi r = 110 \\
   \to r = \dfrac{{110}}{\pi } \\
  \pi = \dfrac{{22}}{7} \\
   \to r = \dfrac{{110}}{{\left( {\dfrac{{22}}{7}} \right)}} = \dfrac{{110 \times 7}}{{22}} \\
   \to r = 5 \times 7 \\
  \therefore r = 35m \\
 $
The radius of the inner circular portion is 35m.
Width of the track w is 14m.
The radius of the outer circular portion R is $R = r + w$
$
  r = 35m,w = 14m \\
  \therefore R = 35 + 14 = 49m \\
 $
The radius of the outer circular portion is 49m.
Length (perimeter) of the outer track is ${P_o} = l + l + \pi R + \pi R$
$
  {P_o} = 90 + 90 + 2\pi R \\
   \to {P_o} = 180 + \left( {2 \times \dfrac{{22}}{7} \times 49} \right) \\
   \to {P_o} = 180 + 308 \\
  \therefore {P_o} = 488m \\
 $
Therefore, the length of the outer track is 488m.
Area of the track is equal to the sum of Area of the two rectangles with measurements 90m×14m (see the diagram) and area of the circular rings
Area of the rectangles is
 $
   = l \times b \\
  l = 90m,b = 14m \\
   \to Are{a_{rectangle}} = 90 \times 14 = 1260{m^2} \\
 $
Area of the circular rings is $\pi \left( {{R^2} - {r^2}} \right)$
$
  r = 35m,R = 49m \\
  \pi \left( {{R^2} - {r^2}} \right) = \pi \left( {{{49}^2} - {{35}^2}} \right) \\
   \to Are{a_{ring}} = \dfrac{{22}}{7}\left( {2401 - 1225} \right) \\
   = \dfrac{{22}}{7} \times 1176 \\
   = 22 \times 168 \\
   = 3696{m^2} \\
 $
Total area of the track is
$
   = \left( {2 \times 1260} \right) + 3696 \\
   = 2520 + 3696 \\
   = 6216{m^2} \\
 $
Therefore, the area of the track is 6216 square meter and the length of the outer track is 488m.

Note: Area is the amount of space which is inside a shape whereas perimeter is the measure of the borders of the shape. Do not confuse between area and perimeter.