Question

The length, breadth and height of a room are 6m, 4.5m and 3m. Find the cost of white washing the walls of the room and the ceiling at the rate of Rupees 8 per m$^2$ .

Answer 1

Hint: According to the question, the room must be a shape of a cuboid. So we must know the properties of the cuboid, its surface area i.e. 2(L x H+ B x H+ L x B). So we have to calculate the area of the room first and then subtract the base area.

Complete Step-by-Step solution:

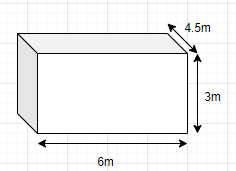
Cuboid is a box shaped object. It has six rectangular faces. Its surface area is calculated by the given below formula-
Surface Area of the cuboid= 2(length x height + breadth x height + length x breadth)
Now using the given Dimensions, we will find the area
 $ \Rightarrow $ Length of the room=6m
 $ \Rightarrow $ Breadth of the room=4.5m
 $ \Rightarrow $ Height of the room=3m
Now in order to calculate the cost of white washing we must know the volume of the room first and then the area of the base so that it could be subtracted from the area which has to be used for white washing.
 Surface area of Cuboid=2(l$ \times $ b + b$ \times $ h + l$ \times $ h)
 $ \Rightarrow $ 2(6$ \times $4.5 + 4.5 $ \times $ 3 + 6 $ \times $ 3)
 $ \Rightarrow $ 2(58.5)
 $ \Rightarrow $ 117

  Now we will find out the area of the base using the formula length $ \times $ breadth
  $ \Rightarrow $ 6$ \times $4.5
  $ \Rightarrow $ 27
 So the required area to be white washed= Area of a cuboid – Area of the base
  $ \Rightarrow $ 117- 27
  $ \Rightarrow $ 90 m$^{^2}$


Also given that cost of white washing per m$^2$ = ₹ 8
$\therefore $ The cost of 90 m$^2$ = 90$ \times $8
 = ₹ 720
So ₹ 720 will be used for white washing of area= 90 m$^{^2}$

Note: Along with this method other ways can also be used to solve this question like area of the four walls and area of the ceiling calculated separately. For that method one must know the formula of the rectangle. One of the important things which most people can omit to do in this question is to subtract the area of base.