Question

The length of a rectangle is four times its width. If the area of the rectangle is \[256{\text{ }}{{\text{m}}^{\text{2}}}\], how do you find its perimeter?

Answer 1

Hint: We have to find the perimeter of the rectangle which has an area of \[256{\text{ }}{{\text{m}}^{\text{2}}}\]. Given that the length of the rectangle is four times its width. We will assume width as \[x\] so length will become \[4x\]. As the area of a rectangle is equal to \[(length \times width)\] i.e., for this case it will be \[\left( {4x \times x} \right)\]. We will equate this area with the given area to find \[x\] and then length and width. Then using the formula Perimeter of a rectangle \[ = 2 \times (length + width)\] we will calculate its perimeter.

Complete step-by-step solution:
Given, the area of the rectangle is \[256{\text{ }}{{\text{m}}^{\text{2}}}\] and the length of the rectangle is four times its width.
Let the width of the rectangle be \[x\], then length will be four times i.e., \[4x\].

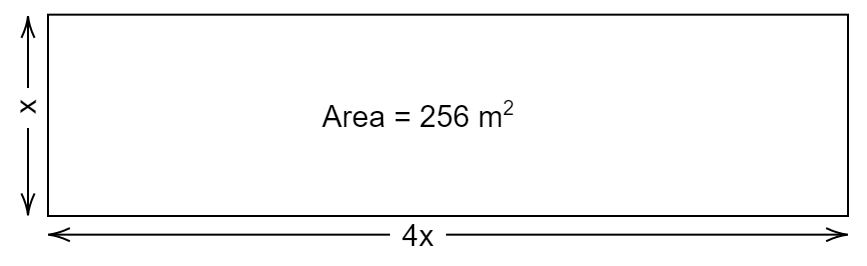
As we know, Area of a rectangle \[ = (length \times width)\]
So, we can write the area of the given rectangle as \[\left( {4x \times x} \right)\] i.e.,
\[ \Rightarrow \] Area of the rectangle \[ = \left( {4x \times x} \right)\]
But, given that area of the rectangle is \[256{\text{ }}{{\text{m}}^{\text{2}}}\]. Therefore, on equating we get
\[ \Rightarrow 256{\text{ }}{{\text{m}}^{\text{2}}} = 4x \times x\]
On dividing both the sides by \[4\] we get
\[ \Rightarrow 64{\text{ }}{{\text{m}}^{\text{2}}} = x \times x\]
On simplification and on rewriting we get
\[ \Rightarrow {\left( x \right)^2} = {\left( {8{\text{ m}}} \right)^{\text{2}}}\]
On simplifying we get,
\[ \Rightarrow x = 8{\text{ m}}\]
\[\therefore Width = 8{\text{ m}}\]
So, \[Length = 4 \times 8{\text{ m}}\] i.e., \[Length = 32{\text{ m}}\].
Now, we know that
Perimeter of a rectangle \[ = 2 \times (length + width)\]
On putting the value of Length and width we get
\[ \Rightarrow {\text{Perimeter of the rectangle}} = 2 \times (32 + 8)\]
On adding the terms in the bracket, we get
\[ \Rightarrow {\text{Perimeter of the rectangle}} = 2 \times (40)\]
On simplification we get
\[ \Rightarrow {\text{Perimeter of the rectangle}} = 80{\text{ m}}\]
Therefore, the perimeter of the rectangle which has area of \[256{\text{ }}{{\text{m}}^{\text{2}}}\] and length four times its width is \[80{\text{ m}}\].

Note: On simplification of \[{x^2} = 64\], we will get two values of \[x\] i.e., \[8\] and \[ - 8\]. But we have not considered \[ - 8\] because distance can never be negative. So, we have discarded that result. Also, when both the dimensions of a rectangle are the same then it becomes square. Its area can be calculated by \[area = {\left( {side} \right)^2}\] and perimeter is calculated by \[perimeter = 4 \times \left( {side} \right)\].