Question

The length of diagonal of a cube is 17.32 cm, find the volume of the cube.

Answer 1

Hint: First, we need to find the length of the diagonal of a cube in terms of its side. Next, find the side of the cube and hence find the volume of the cube.

Complete step by step answer:
The formula of the length \[D\] of the diagonal of the cube is shown below.

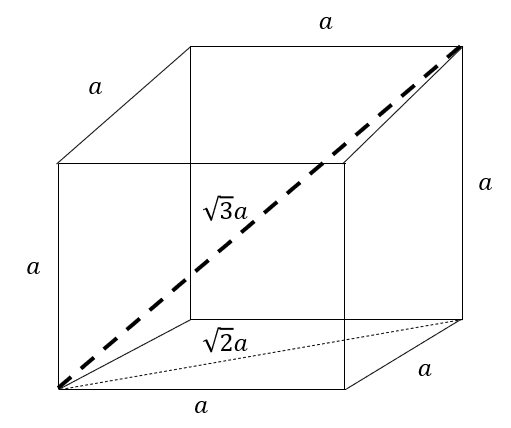
\[D = \sqrt 3 a\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,......\left( 1 \right)\]
Here, \[a\] is the length of the side of the cube.
Since, the diagonal of the cube is 17.32 cm, substitute 17.32 for \[D\] in equation (1) to obtain the length of the side of the cube.
\[
  \,\,\,\,\,\,17.32 = \sqrt 3 a \\
   \Rightarrow a = \dfrac{{17.32}}{{\sqrt 3 }} \\
   \Rightarrow a = \dfrac{{17.32}}{{1.732}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {\sqrt 3 = 1.732} \right) \\
   \Rightarrow a = 10cm \\
\]
The formula for the volume \[V\] of the cube having side length \[a\] is shown below.
\[V = {a^3}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,......\left( 2 \right)\]
Substitute, 10 for \[a\] in equation (2) to obtain the volume of the cube as follows:
\[
  \,\,\,\,\,\,V = {\left( {10} \right)^3} \\
   \Rightarrow V = 1000c{m^3} \\
\]

Thus, the volume of the cube is \[1000c{m^3}\].

Note: We can use Pythagoras theorem to obtain the length of the diagonal of the cube. In the cube all the diagonals are of equal length. There are six face diagonals of the cube having length 1.414 times its side length.