Question

The length of ${\text{fcc}}$ cell is ${\text{508 pm}}$. If the radius of the cation is ${\text{110 pm}}$, the radius of the anion is?
A. ${\text{110 pm}}$
B. ${\text{220 pm}}$
C. ${\text{285 pm}}$
D. ${\text{144 pm}}$

Answer 1

Hint: In ${\text{fcc}}$ cell the cations are present in the octahedral void and the anions are present in the corners of the lattice. Octahedral voids are located in the edges, and along the body diagonal of the cubic lattice.

Complete step by step answer: In ${\text{fcc}}$ lattice atoms are at each corner of the cubic lattice, and also at the face centres. Considering one square face of the cube, corners atoms have contribution equal to the quadrant of a circle, and the face centre atoms contribute equal to a full circle area as shown in the given figure below.

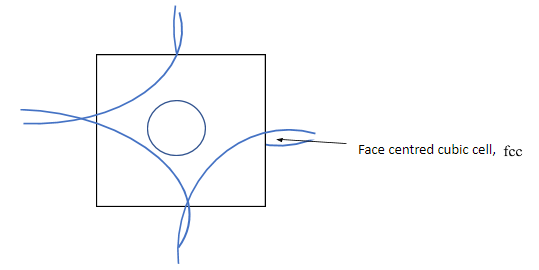
Let ${r^ + }$ be the radius of cation, ${r^ - }$ be the radius of anion, and $a$ be the edge length of the cubic cell. Then from the figure given below, as anions are at the corners of the cube, so, each edge has the anionic radii of ${r^ - } + {r^ - } = 2{r^ - }$, and as cations are at the octahedral voids, which are also in the edges, so each edge will have cationic radii of ${r^ + } + {r^ + } = 2{r^ + }$. Hence, length of an edge will be equal to ${r^ - } + {r^ - } + {r^ + } + {r^ + } = a \Rightarrow a = 2{r^ - } + 2{r^ + }$ ……… $\left( 1 \right)$

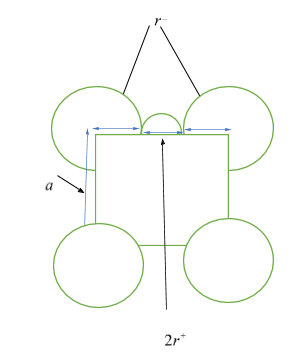
It is given in the question the edge length of the cube, ${\text{a = 508 pm}}$, and radius of the cation, ${r^ + }{\text{ = 110 pm}}$ , so, putting these values in equation $\left( 1 \right)$, we get,
$a = 2{r^ - } + 2{r^ + }$
$ \Rightarrow 508 = 2{r^ - } + 2 \times 110$

$ \Rightarrow 2{r^ - } = 508 - 220$
$ \Rightarrow {r^ - } = \dfrac{{288}}{2}$
${\text{ = 144 pm}}$
= Radius of anion.
Hence, option (d) is the correct answer.

Note: A ${\text{fcc}}$ lattice is consist of two voids, namely, octahedral and tetrahedral void, and the number of tetrahedral voids are twice the number of octahedral voids, so, in the case of tetrahedral void, the relation between the radius of cation, and anion, and the edge length is given by $\dfrac{{\sqrt 3 a}}{4} = {r^ + } + {r^ - }$.