Question

The length of the diagonals of a rhombus is 24cm and 18cm. Find the length of each side of the rhombus.

Answer 1

Hint:Calculate the half-length of both the diagonals of the rhombus. Use the fact that the diagonals of a rhombus bisect each other and then use Pythagoras Theorem to calculate the length of each side of the rhombus.

Complete step-by-step answer:
We have to calculate the length of each side of a rhombus whose diagonals are of length 18cm and 24cm.
We will consider the rhombus ABCD whose diagonals intersect at point O such that $BD=24cm$ and $AC=18cm$, as shown in the figure.

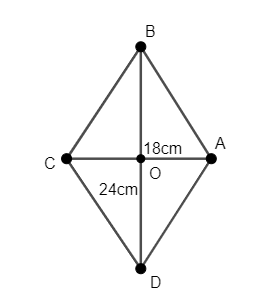
We will first calculate the half-length of both the diagonals of the rhombus.
We know that the diagonals of a rhombus bisect each other.
Thus, we have $OB=OD=\dfrac{24}{2}=12cm$ and $OA=OC=\dfrac{18}{2}=9cm$.
As the diagonals bisect each other, we have $OA\bot OB$. Thus, $\Delta OAB$ is a right-angled triangle.
We will now use Pythagoras Theorem to calculate the length of each side of the rhombus.
We know that Pythagoras Theorem states that in a right-angled triangle, the sum of squares of two perpendicular sides is equal to the square of the third side.
Thus, in $\Delta OAB$, we have ${{\left( OA \right)}^{2}}+{{\left( OB \right)}^{2}}={{\left( AB \right)}^{2}}$.
Substituting $OA=9cm,OB=12cm$ in the above formula, we have ${{\left( 12 \right)}^{2}}+{{9}^{2}}=A{{B}^{2}}$.
Thus, we have $A{{B}^{2}}={{12}^{2}}+{{9}^{2}}=144+81=225$.
Taking square root on both sides, we have $AB=\sqrt{225}=15cm$.
We know that the length of all sides of a rhombus is equal. Thus, we have $AB=BC=CD=AD=15cm$.
Hence, the length of each side of the rhombus is 15cm.

Note: We can calculate the length of each side of rhombus by applying Pythagoras Theorem in any of the right-angled triangles. We will get the same answer in each case. We don’t have to calculate the length of each side of the rhombus. We can simply use the fact that the length of all sides of a rhombus is equal.Remember that the length of diagonals of rhombus are always different and they only bisect with each other.