
The length of the optical path of two media in contact of lengths
Answer
448.8k+ views
Hint: In order to solve this question, we are going to first see what an optical path actually is and then find the optical paths for the two mediums
The optical path of a medium of refractive index
Complete step by step solution:
First of all let us see what an optical path means
The optical path can be defined as the product of the geometrical length of the original path followed by light through a given system and the refractive index of the medium through which it propagates.
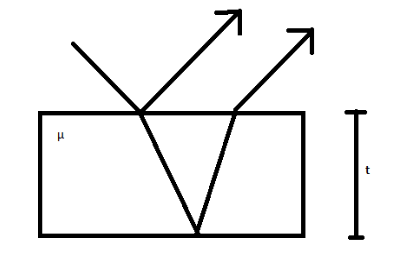
Where,
Thus, in medium 1, the thickness is
In medium 2, the thickness is
Now, to find the optical path of the two media, we will have to add the two optical paths as obtained above, thus, the optical path becomes
Therefore, the total length becomes
Hence, option
Note:
This is the optical path length and not to be confused with the optical path difference at any cost. The expression for the optical path difference is
The optical path of a medium of refractive index
Complete step by step solution:
First of all let us see what an optical path means
The optical path can be defined as the product of the geometrical length of the original path followed by light through a given system and the refractive index of the medium through which it propagates.

Where,
Thus, in medium 1, the thickness is
In medium 2, the thickness is
Now, to find the optical path of the two media, we will have to add the two optical paths as obtained above, thus, the optical path becomes
Therefore, the total length becomes
Hence, option
Note:
This is the optical path length and not to be confused with the optical path difference at any cost. The expression for the optical path difference is
Latest Vedantu courses for you
Grade 10 | CBSE | SCHOOL | English
Vedantu 10 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹37,300 per year
Recently Updated Pages
Master Class 4 Maths: Engaging Questions & Answers for Success

Master Class 4 English: Engaging Questions & Answers for Success

Master Class 4 Science: Engaging Questions & Answers for Success

Class 4 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE




