
The length of the projection of the line segment joining the points (5, -1, 4) and (4, -1, 3) on the plane
Answer
508.2k+ views
2 likes
Hint: First of all, we will find the angle between the plane and the line joining the given two points, using the formula given as follows:
Where,
Complete step-by-step answer:
We have been asked, to find the projection of the line segment joining the point (5, -1, 4) and (4, -1, 3) on the plane
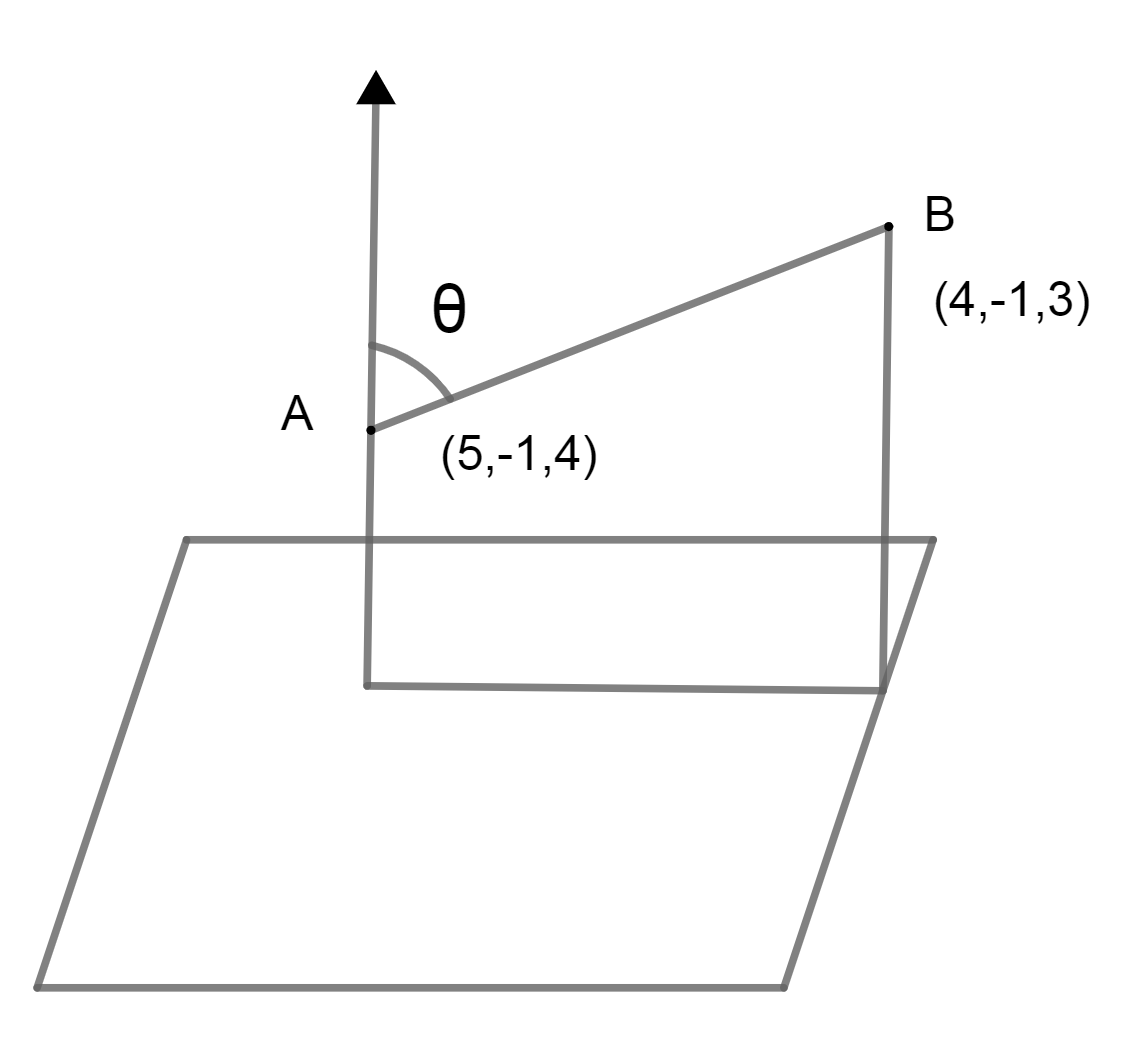
We know that, direction ratio of a is equal to the difference of their respective coordinates.
Direction ratio of line joining points A and B is given by,
Now, the equation of the plane is
Using the formula,
Here, we have,
Multiplying the numerator and denominator with 2, we get,
Cancelling similar terms, we get,
Using the distance formula between the two points i.e.
We can clearly see that, the projection of the line segment AB on the plane is equal to
Using,
Therefore, the correct option is A.
Note: The diagram is very important in this question, as it will help you to think how to proceed further, to get the required result.
Be careful while finding the projection because sometimes we just miss the square root over 2 and choose the answer as
Where,
Complete step-by-step answer:
We have been asked, to find the projection of the line segment joining the point (5, -1, 4) and (4, -1, 3) on the plane

We know that, direction ratio of a is equal to the difference of their respective coordinates.
Direction ratio of line joining points A and B is given by,
Now, the equation of the plane is
Using the formula,
Here, we have,
Multiplying the numerator and denominator with 2, we get,
Cancelling similar terms, we get,
Using the distance formula between the two points i.e.
We can clearly see that, the projection of the line segment AB on the plane is equal to
Using,
Therefore, the correct option is A.
Note: The diagram is very important in this question, as it will help you to think how to proceed further, to get the required result.
Be careful while finding the projection because sometimes we just miss the square root over 2 and choose the answer as
Latest Vedantu courses for you
Grade 10 | CBSE | SCHOOL | English
Vedantu 10 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹37,300 per year
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Draw ray diagrams each showing i myopic eye and ii class 12 physics CBSE

Why do the transition elements have higher enthalpies class 12 chemistry CBSE

What are the advantages of parallel combination over class 12 physics CBSE

What are the causes of overloading class 12 physics CBSE

How do you convert from joules to electron volts class 12 physics CBSE

There is hypertension due to smoking Give scientific class 12 biology CBSE




