Question

The length $x$ of a rectangle is decreasing at the rate of 5 cm/minute and the width $y$ is increasing at the rate of 4 cm/minute. When $x=8$cm and $y=6$cm; find the rates of change of (a) perimeter, and (b) the area of the rectangle. \[\]

Answer 1

Hint: We use the fact that rate of change can be expressed in terms of derivative with respect to time variable $t$ as $\dfrac{d}{dt}x\left( t \right)=-5\text{ cm/minute,}\dfrac{d}{dt}y\left( t \right)=4\text{ cm/minute}$. We use the formula for perimeter of rectangle $P\left( t \right)=P\left( x\left( t \right),y\left( t \right) \right)=2\left( x\left( t \right)+y\left( t \right) \right)$ and differentiate with respect to $t$. We use the formula for area of rectangle $A\left( t \right)=A\left( x\left( t \right),y\left( t \right) \right)=x\left( t \right)\cdot y\left( t \right)$ and then differentiate with respect to $t$. We put $x\left( t \right)=8$cm and $y\left( t \right)=6$cm to get the answers. \[\]

Complete step by step answer:
We are given the question that the length $x$ of a rectangle is decreasing at the rate of 5 cm/minute and the width $y$ is increasing at the rate of 4 cm/minute. Let us denote the variable of time with respect to whom both length and breadth are decreasing as $t$. Here length and breadth are functions of time$x\left( t \right),y\left( t \right)$. So from the definition of derivative as rate of change we have;
\[\begin{align}
  & \dfrac{d}{dt}x\left( t \right)=-5\text{ cm/minute} \\
 & \dfrac{d}{dt}y\left( t \right)=4\text{ cm/minute} \\
\end{align}\]

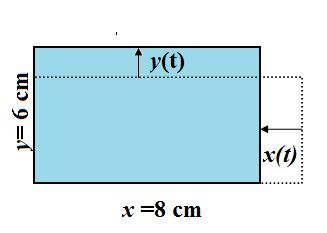
(i)We know that the perimeter of a rectangle is twice the sum of length and breadth. If we denote the perimeter of rectangle at any point of time $t$as $P\left( t \right)$, we have;
\[P\left( t \right)=P\left( x\left( t \right),y\left( t \right) \right)=2\left( x\left( t \right)+y\left( t \right) \right)\]
Let us differentiate the above equation with respect to $t$to find the rate of change of perimeter at any time $t$as
\[\begin{align}
  & \dfrac{d}{dt}P\left( t \right)=\dfrac{d}{dt}2\left( x\left( t \right)+y\left( t \right) \right) \\
 & \Rightarrow \dfrac{d}{dt}P\left( t \right)=2\left( \dfrac{d}{dt}x\left( t \right)+\dfrac{d}{dt}y\left( t \right) \right) \\
 & \Rightarrow \dfrac{d}{dt}P\left( t \right)=2\left( -5+4 \right)=-2 \\
\end{align}\]
So the rate of change of perimeter of rectangle is $x=8$cm and $y=6$cm is $-2$ cm/minute since rate of change is independent of $x\left( t \right),y\left( t \right)$.\[\]
(ii) We know that the area of the rectangle is a product of length and breadth. Let the area function depending on time be $A\left( t \right)$. So we have;
\[A\left( t \right)=A\left( x\left( t \right),y\left( t \right) \right)=x\left( t \right)y\left( t \right)\]
Let us differentiate the above equation with respect to $t$to find the rate of change of perimeter at any time $t$as
\[\begin{align}
  & \dfrac{d}{dt}A\left( t \right)=\dfrac{d}{dt}\left( x\left( t \right)\cdot y\left( t \right) \right) \\
 & \Rightarrow \dfrac{d}{dt}A\left( t \right)=x\left( t \right)\dfrac{d}{dt}y\left( t \right)+y\left( t \right)\dfrac{d}{dt}x\left( t \right) \\
 & \Rightarrow \dfrac{d}{dt}A\left( t \right)=x\left( t \right)\cdot 4+y\left( t \right)\cdot \left( -5 \right) \\
 & \Rightarrow \dfrac{d}{dt}A\left( t \right)=4x\left( t \right)-5y\left( t \right) \\
\end{align}\]
So the rate of change of area of rectangle is $x=8$ cm and $y=6$ cm is
\[\Rightarrow {{\left. \dfrac{d}{dt}A\left( t \right) \right|}_{x\left( t \right)=8,y\left( t \right)=6}}=4\times 8-5\times 6=32-30=2\text{ c}{{\text{m}}^{2}}\text{/minute}\]

Note: We note that the negative sign is used to symbolize decrease. Here the perimeter is decreasing at the rate of 2 cm/minute but is increasing at the rate of $2\text{ c}{{\text{m}}^{2}}/\text{minute}$. We also note that the length, breadth and perimeter constant rate of change at any point of time but area has variable rate of change. We used the product rule here which is defined for differentiable functions $f\left( x \right),g\left( x \right)$ as $\dfrac{d}{dx}\left( f\left( x \right)g\left( x \right) \right)=f\left( x \right)\dfrac{d}{dx}g\left( x \right)+g\left( x \right)\dfrac{d}{dx}f\left( x \right)$.