Question

The lengths of the diagonals of a rhombus are 60 cm and 80 cm. Find the perpendicular distance between the opposite sides of rhombus.

Answer 1

Hint: All sides are equal in a rhombus. So first find the length of the side of the rhombus using Pythagoras theorem. Next find the area of the rhombus using the area of the rhombus by the lengths of diagonals formula. We can also find the area of the rhombus using side and height. So equate the previously obtained area using diagonals to the area using side and height to find the height (perpendicular distance between opposite sides).
Formulas used:
Area of a rhombus is $ \dfrac{1}{2} \times {d_1} \times {d_2} $ , where $ {d_1},{d_2} $ are the diagonals.
Area of a rhombus with side s and height h is $ s \times h $

Complete step by step solution:
We are given that the lengths of the diagonals of a rhombus are 60 cm and 80 cm.

Rhombus is a quadrilateral having the length of all the sides equal. So as we can see in the above diagram, AB, BC, CD and AD are the sides; AC and BD are the diagonals and EF is the height.
AB=BC=CD=AD.
Area of the rhombus when diagonals are given is $ \dfrac{1}{2} \times {d_1} \times {d_2} $ , $ {d_1} = 60\;cm,{d_2} = 80\;cm $
 $ Are{a_{rhombus}} = \dfrac{1}{2} \times 60 \times 80 = 2400\;c{m^2} \Rightarrow eq\left( 1 \right) $
We know that diagonals of a rhombus bisect each other. This means AO=OC=30cm, DO=OB=40cm
Diagonals divide the rhombus into four right angled triangles.

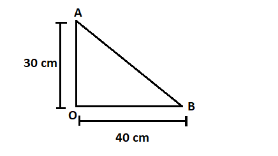
As we can see in the above diagram, AOB is a right triangle and AB is the length of the side.
By Pythagoras theorem, $ A{B^2} = A{O^2} + O{B^2} $
 $ \Rightarrow A{B^2} = {30^2} + {40^2} = 900 + 1600 = 2500 $
 $ \Rightarrow AB = \sqrt {2500} = 50\;cm $
We have got the length of the side of the rhombus.
Area of the rhombus when side and height are given is $ s \times h $
 $ Are{a_{rhombus}} = 50 \times h = 50h \Rightarrow eq\left( 2 \right) $
In either case, the area of the rhombus remains the same; this means equations 1 and 2 are equal.
 $ \Rightarrow 2400 = 50h $
 $ \Rightarrow h = \dfrac{{2400}}{{50}} = 48\;cm $
Therefore, the perpendicular distance (height) between the opposite sides of the rhombus is 48 cm
So, the correct answer is “48 cm”.

Note: According to Pythagoras theorem, hypotenuse square is equal to the sum of squares of the remaining two adjacent sides. Pythagora's theorem can only be applied in right triangles. Bisecting is dividing a line or a shape into two equal parts. All the sides and only opposite angles are equal in a rhombus whereas in a square all the sides and angles are equal. So do not confuse a rhombus with a square.