
The line \[2y - 5 = 0\] is parallel to the \[x\] axis. If true enter 1 else 0.
Answer
552.9k+ views
Hint: Here we will use the basic Cartesian plane to draw the line on the graph. First, we will modify the equation to get it in the linear form. So, we will draw the line with the given equation to find whether the line is parallel to the X-axis or not.
Complete step by step solution:
The given equation of the line is \[2y - 5 = 0\].
First, we will rewrite the given equation to get it in the linear form. Therefore, we get
\[ \Rightarrow 2y = 5\]
\[ \Rightarrow y = \dfrac{5}{2} = 2.5\]
We can see that in the linear equation of the line there is no term of \[x\] which means that for any value of \[x\] the value of \[y\] remains constant. So we will plot this lint on the Cartesian plane.
It is given that the line is passing through the point having \[y\] coordinates as \[2.5\]. The line will be passing through the point which is at a distance of \[2.5\] on the Y-axis from the origin. This line will be parallel to the X-axis as the value of \[y\] will be constant irrespective of the value of \[x\].
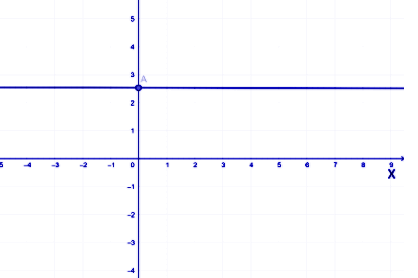
Hence, on the above graph line \[2y - 5 = 0\] is represented.
Note:
We should know that this axis is the infinite lines in the Cartesian plane. While writing the coordinates of a point always the X-axis intercept of the point is written first and then the Y-axis intercept is written. Also in the representation of this axis in the Cartesian plane are perpendicular to each other and intersecting at a point which is named as the origin. We should remember that the positive X-axis is towards the right side of the origin and the negative X-axis is towards the left side of the origin. Also the positive Y-axis is towards the upward direction from the origin and negative Y-axis is towards the downward direction from the origin.
Complete step by step solution:
The given equation of the line is \[2y - 5 = 0\].
First, we will rewrite the given equation to get it in the linear form. Therefore, we get
\[ \Rightarrow 2y = 5\]
\[ \Rightarrow y = \dfrac{5}{2} = 2.5\]
We can see that in the linear equation of the line there is no term of \[x\] which means that for any value of \[x\] the value of \[y\] remains constant. So we will plot this lint on the Cartesian plane.
It is given that the line is passing through the point having \[y\] coordinates as \[2.5\]. The line will be passing through the point which is at a distance of \[2.5\] on the Y-axis from the origin. This line will be parallel to the X-axis as the value of \[y\] will be constant irrespective of the value of \[x\].

Hence, on the above graph line \[2y - 5 = 0\] is represented.
Note:
We should know that this axis is the infinite lines in the Cartesian plane. While writing the coordinates of a point always the X-axis intercept of the point is written first and then the Y-axis intercept is written. Also in the representation of this axis in the Cartesian plane are perpendicular to each other and intersecting at a point which is named as the origin. We should remember that the positive X-axis is towards the right side of the origin and the negative X-axis is towards the left side of the origin. Also the positive Y-axis is towards the upward direction from the origin and negative Y-axis is towards the downward direction from the origin.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




