
The magnitude of
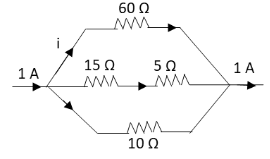

Answer
476.7k+ views
Hint:Divide the given circuit into loops divided by the central wire constituting two resistors. Apply Kirchhoff’s voltage law to these two loops and derive the equations in terms of currents. Also, use the equation for Kirchhoff’s current law to the whole loop and solve the equation obtained to determine the current in the circuit.
Complete step by step answer:
Divide the above given circuit into two loops such as upper loop and lower loop.The current of 1 A gets divided into three branches of the circuit as
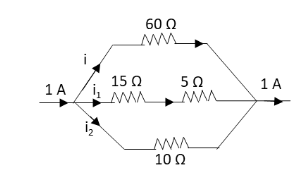
Apply Kirchhoff’s current law to the above circuit.
Apply Kirchhoff’s voltage law to the upper loop of the circuit.
Apply Kirchhoff’s voltage law to the lower loop of the circuit.
Substitute
Substitute
Hence, the current
Additional information:
According to Kirchhoff current law the sum of all the currents flowing into a junction or node is equal to the sum of all the currents coming out of the junction.According to Kirchhoff’s voltage law the sum of all the voltage drops into a loop is equal to zero.
Note: The students should be careful while applying Kirchhoff’s voltage law to the loops in the circuit. The students should always remember that the sign of the voltage term will be positive if the direction of the loop is opposite to the direction of current and negative if the direction of loop is along the direction of the current.
Complete step by step answer:
Divide the above given circuit into two loops such as upper loop and lower loop.The current of 1 A gets divided into three branches of the circuit as

Apply Kirchhoff’s current law to the above circuit.
Apply Kirchhoff’s voltage law to the upper loop of the circuit.
Apply Kirchhoff’s voltage law to the lower loop of the circuit.
Substitute
Substitute
Hence, the current
Additional information:
According to Kirchhoff current law the sum of all the currents flowing into a junction or node is equal to the sum of all the currents coming out of the junction.According to Kirchhoff’s voltage law the sum of all the voltage drops into a loop is equal to zero.
Note: The students should be careful while applying Kirchhoff’s voltage law to the loops in the circuit. The students should always remember that the sign of the voltage term will be positive if the direction of the loop is opposite to the direction of current and negative if the direction of loop is along the direction of the current.
Recently Updated Pages
Master Class 4 Maths: Engaging Questions & Answers for Success

Master Class 4 English: Engaging Questions & Answers for Success

Master Class 4 Science: Engaging Questions & Answers for Success

Class 4 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE




