
The maximum voltage drop across inductance is
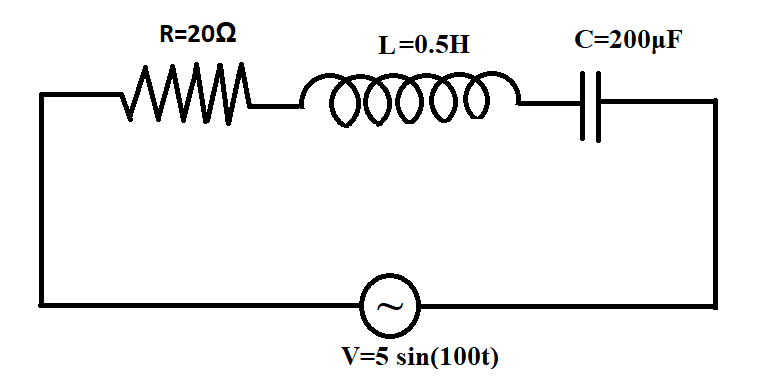
A) $50 Volt$
B) $25 Volt$
C) $12.5 Volt$
D) $5 Volt$
Answer
116.7k+ views
Hint: In this question, we have to use the equations for the series LCR circuit. To find voltage drop we have to multiply the total current with the total resistance of the circuit. In an LCR circuit, the net effective resistance is offered by the combination of resistor, inductor, and capacitor and this is known as the impedance of the circuit.
Formula used:
i) $V = {V_0}\sin \omega t$ (Where V stands for the applied voltage, ${V_0}$ is the peak value of voltage, $\omega = 2\pi f$, where f stands for the frequency of ac)
ii) ${X_L} = \omega L$ (${X_L}$Stands for the inductive resistance, L stands for the inductance of the circuit)
iii) ${X_c} = \dfrac{1}{{\omega C}}$ (${X_C}$ stands for the capacitive reactance, C stands for the capacitance of the circuit)
iv) $Z = \sqrt {{R^2} + {{({X_L} - {X_c})}^2}} $ (Z stands for the impedance of the circuit, R stands for the resistance of the circuit)
v) $I = \dfrac{{{V_0}}}{Z}$ (Where I stands for the current)
vi) ${V_{{X_L}}} = I{X_L}$(where ${V_{{X_L}}}$stands for the voltage drop across the inductance)
Complete step by step solution:
We know that, $V = {V_0}\sin \omega t$ …………………...……………………….(1)
In the question, it is given $V = 5\sin (100t)$……………………..(2)
Comparing $(1)$ and $(2)$ we get,
${V_0} = 5volt$ and $\omega = 100$ (We need these values for the calculation of Inductive resistance, capacitive reactance and maximum current)
Now, we have to find the impedance of the circuit. To find the impedance, we have to find the inductive resistance and the capacitive reactance using the formulae given above)
The inductive resistance, ${X_L} = \omega L$
$\because \omega = 100,L = 0.5H$
${X_L} = 100 \times 0.5 = 50$
The capacitive reactance, ${X_c} = \dfrac{1}{{\omega C}}$
$\because \omega = 100,C = 200 \times {10^{ - 6}}$
${X_c} = \dfrac{1}{{100 \times 200 \times {{10}^{ - 6}}}} = 50$
We have calculated the net resistance offered by the inductor i.e. the inductive resistance and the net resistance offered by the capacitor i.e. the capacitive reactance using their respective formulae.
From the question, $R = 20\Omega $
Now we have the values of ${X_{L,}}{X_c} \& R$ to calculate impedance.
$Z = \sqrt {{R^2} + {{({X_L} - {X_c})}^2}} $
$\because {X_L} = 50,{X_C} = 50\& R = 20$
$Z = \sqrt {{{20}^2} + {{(50 - 50)}^2}} $
$ \Rightarrow Z = \sqrt {{{20}^2} + 0} $
$ \Rightarrow Z = \sqrt {{{20}^2}} = 20$
Using the equation of impedance, we have calculated Z, now we have to find the maximum current through the circuit using the formula, $I = \dfrac{{{V_0}}}{Z}$
$\because {V_0} = 5,Z = 20$
$I = \dfrac{5}{{20}} = 0.25 A$
We know that the formula for current is \[I = \dfrac{V}{R}\].
Since the net effective resistance offered by the circuit is Z we have to use Z to find the maximum current instead of R.
Now we have all the values required to find the voltage drop across the inductance. The voltage drop is obtained by multiplying the total current with the inductive resistance.
${V_{{X_L}}} = I{X_L}$
${V_{{X_L}}} = 0.25 \times 50 $
${V_{{X_L}}} = 12.5 Volt$
The answer is (C) $12.5 Volt$.
Note: While solving units of resistance, capacitance and inductance should be taken care of. Always convert the given value of resistance into units of $\Omega $ (for example if resistance is given in Kilo $\Omega $ convert into $\Omega$ before using in the formula) same applies for inductance and capacitance as well.
Formula used:
i) $V = {V_0}\sin \omega t$ (Where V stands for the applied voltage, ${V_0}$ is the peak value of voltage, $\omega = 2\pi f$, where f stands for the frequency of ac)
ii) ${X_L} = \omega L$ (${X_L}$Stands for the inductive resistance, L stands for the inductance of the circuit)
iii) ${X_c} = \dfrac{1}{{\omega C}}$ (${X_C}$ stands for the capacitive reactance, C stands for the capacitance of the circuit)
iv) $Z = \sqrt {{R^2} + {{({X_L} - {X_c})}^2}} $ (Z stands for the impedance of the circuit, R stands for the resistance of the circuit)
v) $I = \dfrac{{{V_0}}}{Z}$ (Where I stands for the current)
vi) ${V_{{X_L}}} = I{X_L}$(where ${V_{{X_L}}}$stands for the voltage drop across the inductance)
Complete step by step solution:
We know that, $V = {V_0}\sin \omega t$ …………………...……………………….(1)
In the question, it is given $V = 5\sin (100t)$……………………..(2)
Comparing $(1)$ and $(2)$ we get,
${V_0} = 5volt$ and $\omega = 100$ (We need these values for the calculation of Inductive resistance, capacitive reactance and maximum current)
Now, we have to find the impedance of the circuit. To find the impedance, we have to find the inductive resistance and the capacitive reactance using the formulae given above)
The inductive resistance, ${X_L} = \omega L$
$\because \omega = 100,L = 0.5H$
${X_L} = 100 \times 0.5 = 50$
The capacitive reactance, ${X_c} = \dfrac{1}{{\omega C}}$
$\because \omega = 100,C = 200 \times {10^{ - 6}}$
${X_c} = \dfrac{1}{{100 \times 200 \times {{10}^{ - 6}}}} = 50$
We have calculated the net resistance offered by the inductor i.e. the inductive resistance and the net resistance offered by the capacitor i.e. the capacitive reactance using their respective formulae.
From the question, $R = 20\Omega $
Now we have the values of ${X_{L,}}{X_c} \& R$ to calculate impedance.
$Z = \sqrt {{R^2} + {{({X_L} - {X_c})}^2}} $
$\because {X_L} = 50,{X_C} = 50\& R = 20$
$Z = \sqrt {{{20}^2} + {{(50 - 50)}^2}} $
$ \Rightarrow Z = \sqrt {{{20}^2} + 0} $
$ \Rightarrow Z = \sqrt {{{20}^2}} = 20$
Using the equation of impedance, we have calculated Z, now we have to find the maximum current through the circuit using the formula, $I = \dfrac{{{V_0}}}{Z}$
$\because {V_0} = 5,Z = 20$
$I = \dfrac{5}{{20}} = 0.25 A$
We know that the formula for current is \[I = \dfrac{V}{R}\].
Since the net effective resistance offered by the circuit is Z we have to use Z to find the maximum current instead of R.
Now we have all the values required to find the voltage drop across the inductance. The voltage drop is obtained by multiplying the total current with the inductive resistance.
${V_{{X_L}}} = I{X_L}$
${V_{{X_L}}} = 0.25 \times 50 $
${V_{{X_L}}} = 12.5 Volt$
The answer is (C) $12.5 Volt$.
Note: While solving units of resistance, capacitance and inductance should be taken care of. Always convert the given value of resistance into units of $\Omega $ (for example if resistance is given in Kilo $\Omega $ convert into $\Omega$ before using in the formula) same applies for inductance and capacitance as well.
Recently Updated Pages
Uniform Acceleration - Definition, Equation, Examples, and FAQs

Young's Double Slit Experiment Step by Step Derivation

How to find Oxidation Number - Important Concepts for JEE

How Electromagnetic Waves are Formed - Important Concepts for JEE

Electrical Resistance - Important Concepts and Tips for JEE

Average Atomic Mass - Important Concepts and Tips for JEE

Trending doubts
JEE Main 2025: Application Form (Out), Exam Dates (Released), Eligibility & More

JEE Main Login 2045: Step-by-Step Instructions and Details

JEE Main Chemistry Question Paper with Answer Keys and Solutions

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

JEE Main 2025: Conversion of Galvanometer Into Ammeter And Voltmeter in Physics

Electric field due to uniformly charged sphere class 12 physics JEE_Main

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Dual Nature of Radiation and Matter Class 12 Notes CBSE Physics Chapter 11 (Free PDF Download)

Charging and Discharging of Capacitor

JEE Mains 2025 Correction Window Date (Out) – Check Procedure and Fees Here!

JEE Main Exam Marking Scheme: Detailed Breakdown of Marks and Negative Marking

Physics Average Value and RMS Value JEE Main 2025




