Question

The measure of two adjacent angles of a quadrilateral are $110^{\circ}$ and $50^{\circ}$ and the other two angles are equal. Find the measure of each angle.

Answer 1

Hint: In this question it is given that the measure of two adjacent angles of a quadrilateral are $110^{\circ}$ and $50^{\circ}$ and the other two angles are equal, i.e, $\angle A=\angle B$. We have to find the measures of those angels. So to understand it in better way we have to draw the diagram,

So to find the solution we have to know that the summation of all the angles of a quadrilateral is $360^{\circ}$.

Complete step-by-step solution:
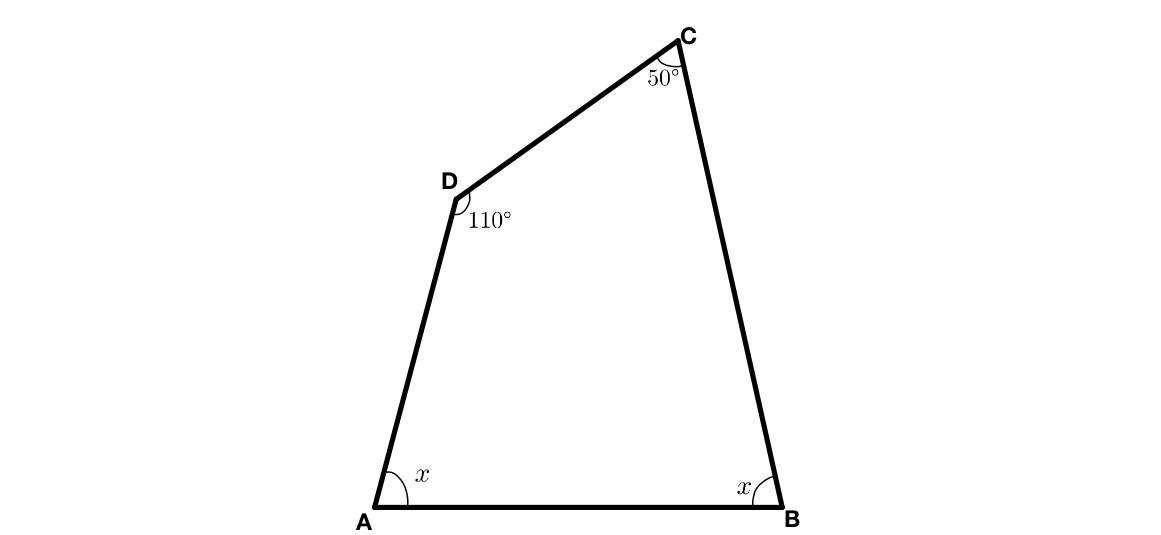
Let ABCD is a quadrilateral, and $$\angle D=110^{\circ}\ and\ \angle C=50^{\circ}$$
Also let $\angle A=\angle B=x$
Now since, the summation of all angles of a quadrilateral is $360^{\circ}$,
Therefore,
$$\angle A+\angle B+\angle C+\angle D=360^{\circ}$$
$$\Rightarrow x+x+110^{\circ}+50^{\circ}=360^{\circ}$$
$$\Rightarrow 2x+160^{\circ}=360^{\circ}$$
$$\Rightarrow 2x=360^{\circ}-160^{\circ}$$
$$\Rightarrow 2x=200^{\circ}$$
$$\Rightarrow x=\dfrac{200^{\circ}}{2}$$
$$\Rightarrow x=100^{\circ}$$
Therefore, the angles are $$\angle A=\angle B=100^{\circ}$$.

Note: In this question it is given that two adjacent angles, so adjacent angles implies two angles when they have a common side. Also for a quadrilateral every angle has only two adjacent angles, like $\angle A$ has two adjacent angles one is $\angle B$ and another one is $\angle D$.