Question

The moment of inertia of a cube of mass M and edge length a about an axis passing through one of its edges is
A. \[\dfrac{M{{a}^{2}}}{6}\]
B. \[\dfrac{M{{a}^{2}}}{3}\]
C. \[\dfrac{M{{a}^{2}}}{2}\]
D. \[\dfrac{2M{{a}^{2}}}{3}\]

Answer 1

Hint: The parallel axis theorem states that the Moment of Inertia of any body about an axis that is parallel to the axis passing through the centre is given by the formula provided. Also, the edge and axis passing through the centre of face and cube is parallel in a cube. And the moment of inertia of a cube of mass M and edge length about an axis passing through one of its centres is given below.

Formula used:
\[I={{I}_{c}}+m{{d}^{2}}\]
\[{{I}_{c}}=\dfrac{M{{a}^{2}}}{6}\] for cube

Complete step by step answer:
We know that the moment of inertia of a cube of mass M and edge length a about an axis passing through one of its centres is
\[{{I}_{c}}=\dfrac{M{{a}^{2}}}{6}\]
And we also know that the parallel axis theorem states that, the moment of Inertia of any body about an axis parallel to the axis passing through centre can be given as the sum of moment of inertia of body about the axis passing through the centre of the body and product of mass of the body times the square of distance between the two axes. It can be formulated as:
\[I={{I}_{c}}+m{{d}^{2}}\], where
 I is the moment of inertia about an axis that is parallel to the axis passing through the centre
\[{{I}_{c}}\]is the moment of inertia about an axis passing through the centre of the body
m is the mass of the body and
d is the distance between the axis passing through the centre and the axis parallel to it
Now coming to our question

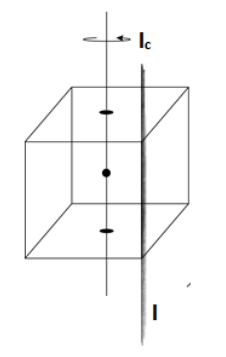
We have \[{{I}_{c}}=\dfrac{M{{a}^{2}}}{6}\] and we need to find I
The distance between the axis and centre of the cube is \[\dfrac{a}{\sqrt{2}}\]
Since, the edge and axis passing through the centre of face and cube is parallel in a cube so we can use parallel theorem, to get I.
Applying parallel theorem, \[I={{I}_{c}}+m{{d}^{2}}\] we get
\[\begin{align}
  & I={{I}_{c}}+M{{d}^{2}} \\
 & \Rightarrow I=\dfrac{M{{a}^{2}}}{6}+M{{\left( \dfrac{a}{\sqrt{2}} \right)}^{2}} \\
 & \Rightarrow I=\dfrac{M{{a}^{2}}}{6}+\dfrac{M{{a}^{2}}}{2} \\
 & \Rightarrow I=\dfrac{2M{{a}^{2}}}{3} \\
\end{align}\]
So, the moment of inertia of a cube of mass M and edge length a about an axis passing through one of its edges is \[\dfrac{2M{{a}^{2}}}{3}\]

So, the correct answer is “Option D”.

Note:
The given question can also be solved with taking the moment of inertia of a cube about an axis passing through one of its centres. We can solve the question by the elementary definition of Moment of inertia by taking a corner of the cube to be on the origin and the distance of every point of the cube from the edge lying concurrent with Z axis would be \[r=\sqrt{{{x}^{2}}+{{y}^{2}}}\]and then we can integrate to find the Moment of inertia about the edge. \[I=\int{{{r}^{2}}dm}\]where dm is the mass of infinitesimal small elements taken for integration.