Question

The moon is observed from two diametrically opposite points A and B on earth. The angle subtended at the moon by two directions of observation is \[{{1}^{0}}54'\]. The diameter of the earth is \[1.276\times {{10}^{7}}m\]. Calculate the distance of the moon from earth.

Answer 1

Hint: We are given the details of an experiment conducted to find the lunar distance from the earth. We need to use the trigonometric relations between the given angle and the distance to find the distance from the moon to our planet earth.

Complete answer:
The moon is the earth’s satellite which revolves around it. The scientists have found the distance to this celestial object and others a long time ago using trigonometry without really being into space. The above details are from such an experiment where we find the distance from the moon to the earth using some known parameters.
We are informed that two teams observe the moon from the diametrically opposite points on the earth, say A and B at the same time as shown in the figure below.

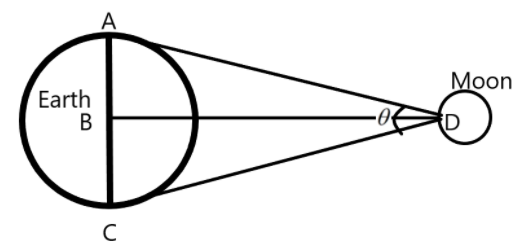
The angle subtended at the moon due to the observation is \[{{1}^{0}}54'\]. Also, the diameter of the earth is given as \[1.276\times {{10}^{7}}m\].
Now, let us consider the above figure as two right angled triangles with the angle at the moon being the half of the original angle subtended. The arm AB and BC of the triangles constitute the radius of the earth, which is half the diameter.

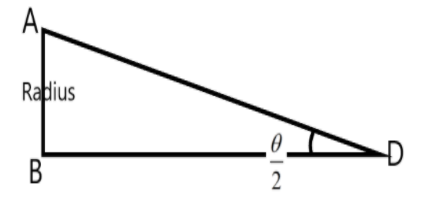
We can use the trigonometric relations to find the distance BD which is the distance from the moon to the earth as –
\[\begin{align}
  & \text{In }\Delta \text{ABD,} \\
 & \tan \dfrac{\theta }{2}=\dfrac{AB}{BD} \\
 & \Rightarrow BD=\dfrac{AB}{\tan \dfrac{\theta }{2}} \\
 & \text{but,} \\
 & AB=\dfrac{1.276\times {{10}^{7}}m}{2}=6.38\times {{10}^{6}}m \\
 & \dfrac{\theta }{2}=\dfrac{{{1}^{0}}54'}{2}=\dfrac{1}{2}(1+\dfrac{54}{60})\dfrac{\pi }{180}rad \\
 & \Rightarrow \dfrac{\theta }{2}=0.0166rad \\
\end{align}\]
We can find the unknown parameter BD as –
\[\begin{align}
  & BD=\dfrac{AB}{\tan \dfrac{\theta }{2}} \\
 & \Rightarrow BD=\dfrac{6.38\times {{10}^{6}}m}{\tan (0.0166)} \\
 & \Rightarrow BD=\dfrac{6.38\times {{10}^{6}}m}{0.0166} \\
 & \therefore BD=3.84337\times {{10}^{8}}m \\
\end{align}\]
The distance from the moon to the earth is 384,337km. This is the required solution.

Note:
The distance we found from the moon to the earth is an average distance which can change during the different phases and position of earth and moon. The trigonometric relation was used by the earlier scientists which gave accurate measurements at each time of the year.