Question

The normal at $ \left( {a,2a} \right) $ on $ {y^2} = 4ax $ meets the curve again at $ \left( {a{t^2},2at} \right) $ . Then the value of its parameter is equal to
A. 1
B. 3
C. -1
D. -3

Answer 1

Hint: First find the slope of the tangent at point $ \left( {a,2a} \right) $ by differentiating the equation $ {y^2} = 4ax $ with respect to x. The slopes of perpendicular lines are negative reciprocals of one another. So using this, find the slope of normal at point $ \left( {a,2a} \right) $ as normal and tangent are perpendicular to each other. Using the slope of the normal line and point $ \left( {a,2a} \right) $ , find the line equation of the normal line. Substitute the line equation in the curve equation $ {y^2} = 4ax $ to find the parameter t.
Formulas used:
Slope-point form of a line equation is $ \left( {y - {y_1}} \right) = m\left( {x - {x_1}} \right) $ , where m is the slope and $ \left( {{x_1},y1} \right) $ is the given point.

Complete step by step solution:
We are given that the normal at $ \left( {a,2a} \right) $ on $ {y^2} = 4ax $ meets the curve again at $ \left( {a{t^2},2at} \right) $ .
We have to find the value of t.
First we have to find the slope of tangent at point $ \left( {a,2a} \right) $ .

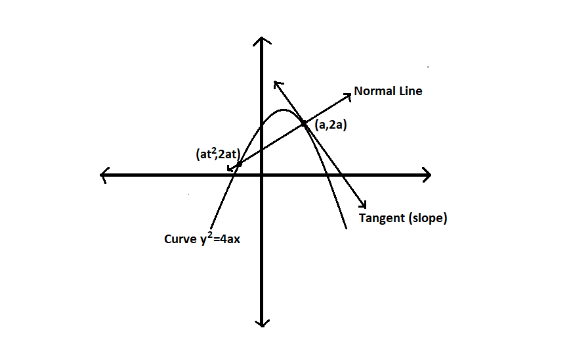
So we are differentiating $ {y^2} = 4ax $ with respect to x.
We get,
 $ \dfrac{d}{{dx}}\left( {{y^2}} \right) = \dfrac{d}{{dx}}\left( {4ax} \right) $
 $ \Rightarrow 2y\dfrac{{dy}}{{dx}} = 4a\left( {\dfrac{{dx}}{{dx}}} \right) $
Let $ \dfrac{{dy}}{{dx}} $ be $ y' $ .
 $ \Rightarrow 2yy' = 4a\left( {\because \dfrac{{dx}}{{dx}} = 1} \right) $
 $ \Rightarrow y' = \dfrac{{4a}}{{2y}} $
Slope of tangent at point $ \left( {a,2a} \right) $ is $ \dfrac{{4a}}{{2\left( {2a} \right)}} = \dfrac{{4a}}{{4a}} = 1 $ as y-coordinate of $ \left( {a,2a} \right) $ is 2a.
Tangent and normal are perpendicular lines. So the slope of the normal line at point $ \left( {a,2a} \right) $ is $ \dfrac{{ - 1}}{{\left( 1 \right)}} = - 1 $
We have got the slope of the normal and the point, $ \left( {a,2a} \right) $ , from which the normal travels.
Therefore, the equation of the normal line is $ \left( {y - {y_1}} \right) = m\left( {x - {x_1}} \right) $
 $ \Rightarrow y - 2a = - 1\left( {x - a} \right) $
 $ \Rightarrow y - 2a = - x + a $
 $ \Rightarrow y = 3a - x $
On substituting the value of y as $ 3a - x $ in $ {y^2} = 4ax $ , we get
 $ \Rightarrow {\left( {3a - x} \right)^2} = 4ax $
 $ \Rightarrow 9{a^2} + {x^2} - 6ax = 4ax $
 $ \Rightarrow {x^2} - 6ax - 4ax + 9{a^2} = 0 $
 $ \Rightarrow {x^2} - 10ax + 9{a^2} = 0 $
We are next finding the factors of the above equation
 $ \Rightarrow {x^2} - ax - 9ax + 9{a^2} = 0 $
 $ \Rightarrow x\left( {x - a} \right) - 9a\left( {x - a} \right) = 0 $
 $ \Rightarrow \left( {x - a} \right)\left( {x - 9a} \right) = 0 $
 $ \therefore x = a,x = 9a $
The value of x is 9a as we already know when x is a, y is 2a in the point $ \left( {a,2a} \right) $
This gives,
 $ y = 3a - x = 3a - 9a = - 6a $
Therefore, the x and y coordinates of point $ \left( {a{t^2},2at} \right) $ are 9a and -6a respectively.
This means that
 $ \Rightarrow 2at = - 6a $
 $ \therefore t = \dfrac{{ - 6a}}{{2a}} = - 3 $
Therefore, the parameter t is equal to -3.
So, the correct answer is option (D), “ -3”.

Note: Here we have a slope and point given so we have used slope-point form to find the line equation of the normal. If two points of a line are given, then we have to use two-point form to find the line equation. A tangent is a straight line to a plane curve at a given point that just touches the curve only at one (given) point. Do not confuse a tangent with a secant.