Question

The number of NaCl units present in a unit cell of NaCl is:
A.1
B.2
C.4
D.8

Answer 1

Hint: In order to solve this problem, we must firstly understand the type of unit cell present in the structure of NaCl. Then we can calculate the total number of atoms present in this unit cell and by relation, correspond the value of the total number of atoms to NaCl.

Complete step by step answer:
NaCl is an ionic crystalline compound. While formation of the crystal structure of sodium chloride, it crystallizes into a packing structure known as face – centred cubic. This packing structure forms a single unit in the multi – molecule lattice structure of sodium chloride. In this type of unit – cell, i.e. face centred cubic, the following characteristics are observed:
In face centred cubic structure, there are atoms on all the vertices of the cube
Atoms are also present on all the sides of the cube
The vertices have $\dfrac{1}{8}$ th of an atom on every vertex due to geometric constraints
Similarly, all faces have only \[\dfrac{1}{2}\] of an atom on every face due to geometric constraints

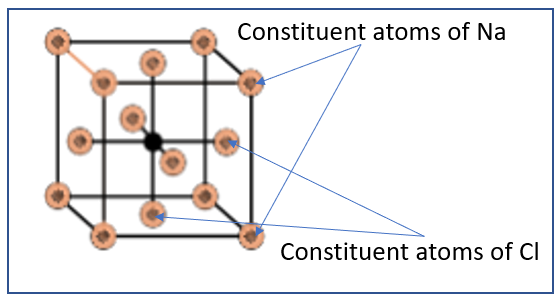
From this, we can infer that there are 8 portions of the $\dfrac{1}{8}$ th of an atom on the 8 vertices of the cube, while all the 6 sides of the cube have ½ atoms each. Hence the total number of atoms present in the face centred cubic structure can be calculated to be:
Total number of atoms = $\dfrac{1}{8}$ (8 vertices) + \[\dfrac{1}{2}\] (6 faces) = 1 + 3 = 4 atoms
Hence, there are 4 atoms present in each unit cell of a face centred cubic structure.
Hence, the number of NaCl units present in a unit cell of NaCl is 4

Hence, Option C is the correct option.

Note:
NaCl has a cubic unit cell that can be represented as a face-centred cubic array of anions with an interpenetrating fcc cation lattice (or vice-versa). This unit cell of NaCl looks the same whether we start with cations or anions at the corners. Each of these ions is 6-coordinate and has a local octahedral geometry.