
The pair of equations
A.Parallel
B.Intersecting at
C.Coincident
D.Intersecting at
Answer
436.6k+ views
2 likes
Hint: The
Complete step-by-step answer:
Before plotting the points , we must know about the coordinate system.
The cartesian coordinate system is a system of identifying the location of a point with respect to two perpendicular lines , known as coordinate axes. The vertical axis is called the
Now, coming to the question, the pair of equations given to us are
This can be represented graphically as:
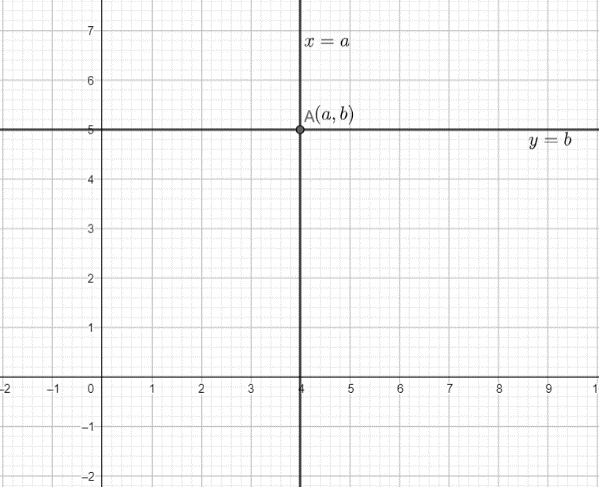
So, the lines
Hence, option D. is the correct option.
Note: Students get confused and write that the line
Complete step-by-step answer:
Before plotting the points , we must know about the coordinate system.
The cartesian coordinate system is a system of identifying the location of a point with respect to two perpendicular lines , known as coordinate axes. The vertical axis is called the
Now, coming to the question, the pair of equations given to us are
This can be represented graphically as:

So, the lines
Hence, option D. is the correct option.
Note: Students get confused and write that the line
Latest Vedantu courses for you
Grade 9 | CBSE | SCHOOL | English
Vedantu 9 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹37,300 per year
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

What are the major means of transport Explain each class 12 social science CBSE

Why is the cell called the structural and functional class 12 biology CBSE




