Question

The path of a projectile is a parabola.
(a) True
(b) False

Answer 1

Hint: To solve this question, we will first define both projectile and parabola and then discuss the relationship between them and finally we will draw the path of the projectile and check if it resembles that of a parabola. In that way, we would be able to answer the question.

Complete step by step answer:
Let us define the parabola first. The parabola is the locus of points in that plane that are equidistant from both the directrix and the focus. Another description of a parabola is a conic section, created from the intersection of a right circular conical surface and a plane parallel to another plane that is tangential to the conical surface. The examples of the standard parabola are:
\[\left( I \right){{y}^{2}}=x\]
It is drawn as

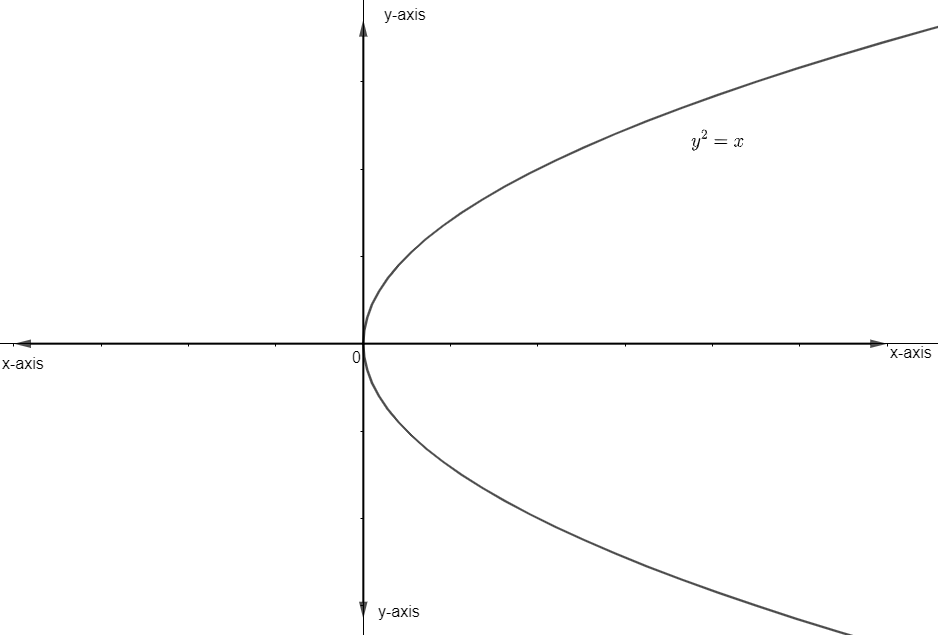
\[\left( II \right)y={{x}^{2}}\]
It is drawn as

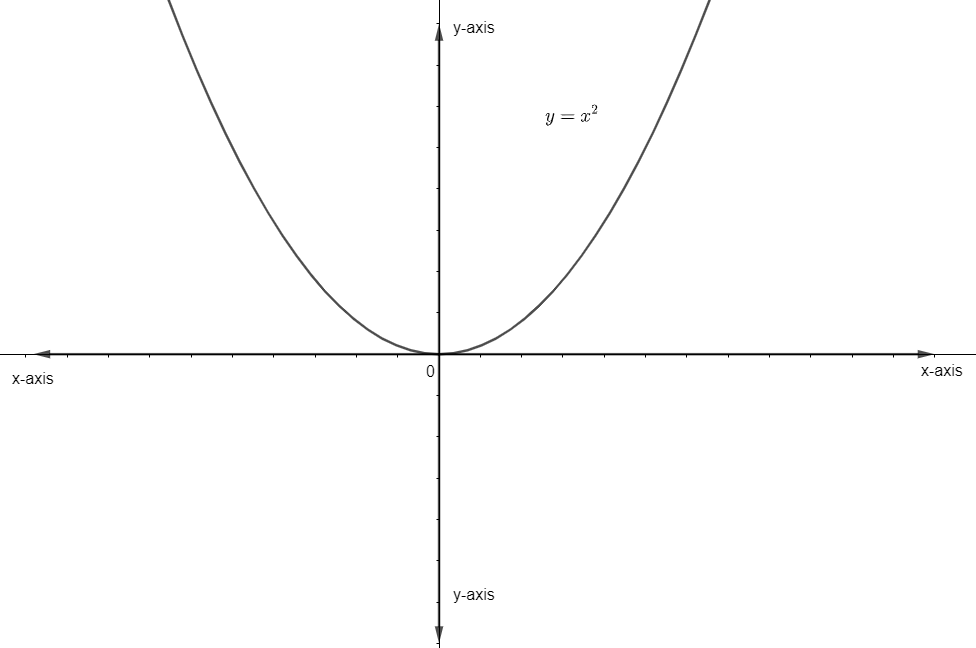
There are some types of parabola stated above. We measure them from the x – axis increasing or decreasing.
Let us now define the projectile and path of the projectile. The projectile motion is a form of the motion experienced by an object or a particle that is projected near the Earth’s surface and moves along a curved path under the action of gravity only. It is a motion of the form

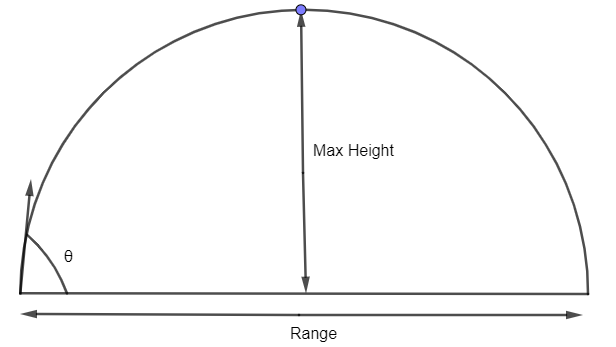
It is a motion that is experienced when for example a ball is thrown up from the ground and then after reaching the maximum height, the ball comes to the ground after a certain time. There is a parabola of the type having the equation given as \[{{x}^{2}}=-4ay\] then the focus is at (0, – a) and vertex, x = (0, 0). And the diagram of that parabola is of the form

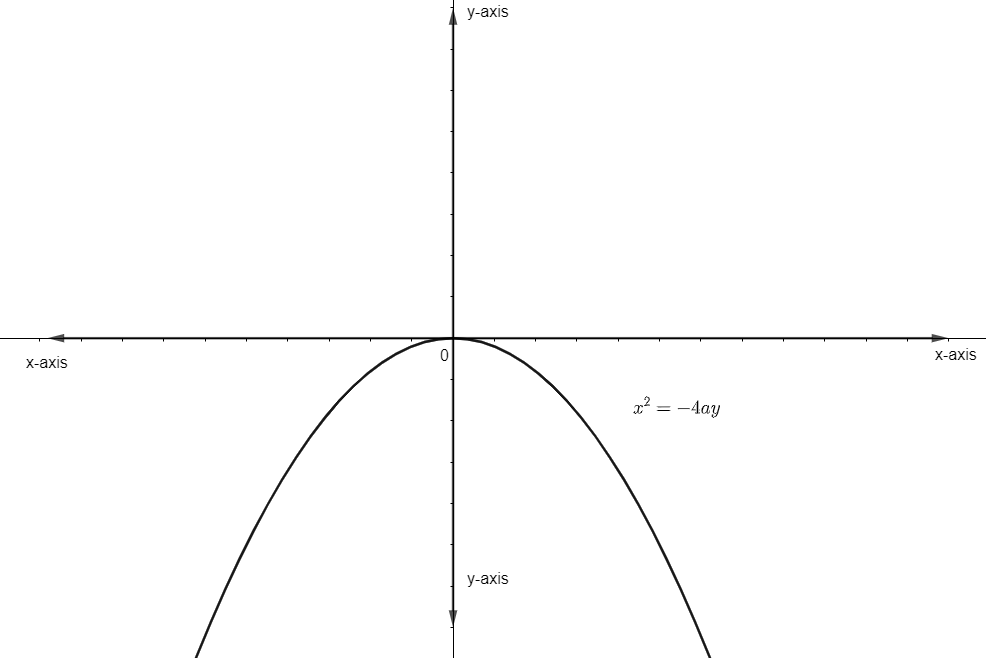
Matching the two figures, we observe that the path of the projectile resembles that of \[{{x}^{2}}=-4ay\] a parabola and hence the path of the projectile is a parabola. Therefore, it is a true statement.

So, the correct answer is “Option a”.

Note: Here in the parabola \[{{x}^{2}}=-4ay\] the axis of the parabola is at x = 0 and the directrix is at y = a. Comparing this with the projectile, the equation of directrix and that of the axis may differ. In fact, the coordinates of the vertex and focus can differ, but the path is always in parabolic form.