Question

The pedal equation of the circle ${{x}^{2}}+{{y}^{2}}=4$ with regard to the point (2,0) is
[a] ${{r}^{2}}=4$
[b] $4p={{r}^{2}}$
[c] ${{p}^{2}}=4r$
[d] $p=4{{r}^{2}}$

Answer 1

Hint: Use the property that the tangent of a circle and the radius are perpendicular to each other at the point of contact. Use the property that angle in a semicircle is a right angle. Hence prove that the angles $\angle \text{ABD}$ and $\angle \text{BCA}$ are equal. Use trigonometry to get a relation between AB, AD and BC. Substitute AD = p, AB = r and BC = 4 to get the required pedal equation.

Complete step-by-step answer:

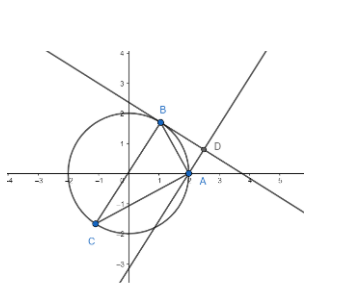
Pedal equation: Definition: Pedal equation of a curve C and given fixed point O is the relation between r and p, where r is the distance if point O to a point on the curve C and p is the perpendicular distance of O from the tangent line drawn at that point. The point O is called the pedal point and the values r and p are known as the pedal coordinates of the curve C w.r.t the pedal point.
Here we have, the pedal point is A (2,0), and B is any point on the locus. BD is the tangent at point B, and AD is the perpendicular from A on BD. C is the diametrically opposite point of B.
Hence, we have AD = p and AB = r.
Since BC is a diameter, we have $\angle \text{BAC=90}{}^\circ $
Let $\angle \text{BCA=}\theta $.
Hence we have
$\angle \text{CBA=90}{}^\circ \text{-}\theta $
Since BD is a tangent and BC is a diameter, we have $\angle \text{CBD=90}{}^\circ $
Hence, we have $\angle \text{ABD=}\theta $
In triangle ABD, we have $\sin \theta =\dfrac{\text{AD}}{\text{AB}}\text{ (i)}$
In triangle ABC, we have $\sin \theta =\dfrac{\text{AB}}{\text{BC}}\text{ (ii)}$
From (i) and (ii), we get
$\dfrac{\text{AD}}{\text{AB}}=\dfrac{\text{AB}}{\text{BC}}$
Since for circle with equation ${{x}^{2}}+{{y}^{2}}={{a}^{2}}$ radius = a, we have BC = 4.
Put AD = p, AB = r and BC = 4, we get
$\begin{align}
  & \dfrac{p}{r}=\dfrac{r}{4} \\
 & \Rightarrow 4p={{r}^{2}} \\
\end{align}$
which is the required pedal equation of the circle.
Hence option [b] is correct.

Note: In the pedal equation, we denote distance of any point on the locus from the pedal point by r and the distance of the pedal point from the tangent at the point on the locus by p. We then find the relation between p and r. This relation is called the pedal equation of the curve.
Alternative Solution:
Pedal equation of a circle with respect to any point on the circumference of the circle is given by $pd={{r}^{2}}$, where d is the diameter of the circle.
Here d = 4.
Hence the pedal equation is $4p={{r}^{2}}$ .