Question

The perimeter of isosceles trapezoid ABCD is 50. If BC=9 and AD=21, calculate the length of diagonal AC.

$
  (a){\text{ 13}} \\
  (b){\text{ 14}} \\
  (c){\text{ 15}} \\
  (d){\text{ 16}} \\
  (e){\text{ 17}} \\
 $

Answer 1

Hint – In this question pictorial representation will help us of what we have to find out so first draw the pictorial representation of the problem then use the concept that in any shape the perimeter is the sum of all the sides and in an isosceles trapezoid the two sides which are non-parallel to each other are equal (i.e. AB = CD) later on using the property of Pythagoras theorem we will reach the solution of the question.

Complete step-by-step answer:

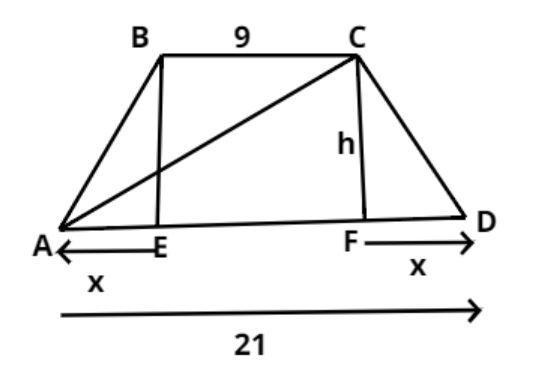
Draw perpendiculars from point B and C on AD which meet at points E and F respectively,
Let BE = CF = h

So by symmetry AE = FD = x and EF = BC = 9

The length of AD = 21 (given).
$ \Rightarrow AD = AE + EF + FD$
So substitute the values we have,
$ \Rightarrow 21 = x + 9 + x$
$ \Rightarrow 2x = 12$
$ \Rightarrow x = 6$

Now it is given that the trapezoid ABCD is isosceles.

Therefore AB = CD (because other two sides are not equal so these two sides should be equal).

And it is also given that the perimeter of isosceles trapezoid ABCD is 50.
$ \Rightarrow AB + BC + CD + DA = 50$

Now substitute the values in this equation we have,
$ \Rightarrow AB + 9 + AB + 21 = 50$
$ \Rightarrow 2AB = 20$
$ \Rightarrow AB = 10 = CD$

Now in triangle CDF apply Pythagoras Theorem we have,
$ \Rightarrow {\left( {{\text{Hypotenuse}}} \right)^2} = {\left( {{\text{perpendicular}}} \right)^2} + {\left( {{\text{base}}} \right)^2}$
$ \Rightarrow {\left( {CD} \right)^2} = {\left( {CF} \right)^2} + {\left( {FD} \right)^2}$

Now substitute the value in this equation we have,
$\begin{gathered}
  \Rightarrow {10^2} = {6^2} + {h^2} \\
  \Rightarrow {h^2} = 100 - 36 = 64 = {8^2} \\
  \Rightarrow h = 8 \\
\end{gathered}$

Now in triangle ACF apply Pythagoras theorem we have,
$ \Rightarrow {\left( {{\text{Hypotenuse}}} \right)^2} = {\left( {{\text{perpendicular}}} \right)^2} + {\left( {{\text{base}}} \right)^2}$
$ \Rightarrow {\left( {AC} \right)^2} = {\left( {CF} \right)^2} + {\left( {AF} \right)^2}$

Now substitute the value in this equation we have,
$ \Rightarrow {\left( {AC} \right)^2} = {h^2} + {\left( {AE + EF} \right)^2} = {8^2} + {\left( {6 + 9} \right)^2} = 64 + 225 = 289 = {\left( {17} \right)^2}$
$ \Rightarrow AC = 17$

So the length of the diagonal AC is 17 units.

Hence option (E) is correct.

Note – whenever we face such types of question the key concept we have to remember is that in an isosceles trapezoid when we draw the perpendiculars from point B and C on the side AB which meet at point E and F respectively than by symmetry BC = EF and AE = FD, so first calculate the distance FD as above then apply the concept of perimeter and calculate the length of non-parallel sides as above then apply Pythagoras Theorem in triangle CFD and calculate the length of the perpendicular as above then apply the Pythagoras theorem in triangle ACF we will get the required value of the diagonal.