Question

The perimeter of sheet of paper in the shape of a quadrant of a circle is \[25\] cm, then the area of the paper is
A. \[\dfrac{{77}}{2}\;c{m^2}\]
B. \[\dfrac{{77}}{2}{\left( {\dfrac{{25}}{{18}}} \right)^2}\;c{m^2}\]
C. \[\dfrac{{231}}{2}\;c{m^2}\]
D. None of these

Answer 1

Hint:Here the perimeter of a sheet of paper which is in the shape of a quadrant circle. By considering the formula of the perimeter of the quadrant circle \[P = 2r + \dfrac{{2\pi r}}{4}\], we determine the value of $r$. Then by considering the formula \[A = \dfrac{1}{4}\left( {\pi {r^2}} \right)\], we are determining the value of the area.

Complete step by step answer:
The quadrant of a circle is represented as

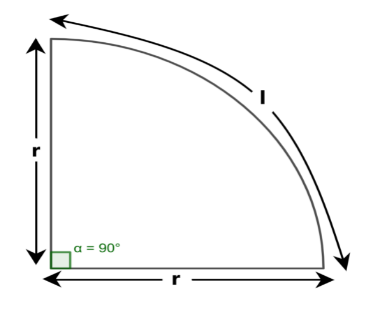
The circle is equal to four quadrants. The perimeter for the quadrant of a circle is given by,
\[P = 2r + \dfrac{{2\pi r}}{4}\]
By using this formula we determine the value of $r$, then we can determine the value of the area. Now consider
\[ \Rightarrow P = 2r + \dfrac{{\pi r}}{2}\]
From the given data we know the value of P and it is given as \[25\] cm , on substituting we have
\[ \Rightarrow 25 = 2r + \dfrac{{\pi r}}{2}\]
As we know that the value of \[\pi = \dfrac{{22}}{7}\]
\[ \Rightarrow 25 = 2r + \left( {\dfrac{{22}}{7}} \right)\dfrac{r}{2}\]
on simplifying we have
\[ \Rightarrow 25 = 2r + \dfrac{{22r}}{{14}}\]
On taking LCM we have
\[ \Rightarrow 25 = \dfrac{{28r + 22r}}{{14}}\]

On multiplying 14 to both sides
\[ \Rightarrow 25 \times 14 = \dfrac{{28r + 22r}}{{14}} \times 14\]
On multiplying we have
\[ \Rightarrow 350 = 28r + 22r\]
On adding 28r and 22r we have
\[ \Rightarrow 350 = 50r\]
On dividing by 50 we have
\[ \Rightarrow r = 7\] cm

Hence we have determined the value of $r$. Now we have to determine the value of the area of the quadrant of a circle. The formula is given by,
\[A = \dfrac{1}{4}\left( {\pi {r^2}} \right)\]
On substituting the value of r in the formula we have
\[ \Rightarrow A = \dfrac{1}{4}\left( {\pi \times 7 \times 7} \right)\]
As we know that the value of \[\pi = \dfrac{{22}}{7}\]
\[ \Rightarrow A = \dfrac{1}{4}\left( {\dfrac{{22}}{7} \times 7 \times 7} \right)\]
On simplifying we have
\[ \Rightarrow A = \dfrac{1}{4}\left( {22 \times 7} \right)\]
\[ \Rightarrow A = \dfrac{{154}}{4}\]
On dividing the both numerator and denominator by 2 we have
\[ \therefore A = \dfrac{{77}}{2}\;c{m^2}\]
Therefore the area of the paper is \[A = \dfrac{{77}}{2}\;c{m^2}\]

Hence the option A is the correct one.

Note:The perimeter and area of a circle is given by \[2\pi r\] and \[\pi {r^2}\]. But for the perimeter and area of a quadrant of a circle is taken one fourth of the perimeter and area of a circle. In the perimeter of the quadrant of a circle we are including \[2r\] because when we see the diagram the part includes two radii.