
The phase difference between current and voltage in an AC circuit is
A). 0.78s
B). 15.7ms
C). 2.5s
D). 2.5ms
Answer
505.5k+ views
Hint: In an AC circuit, the voltage and the current are treated as vectors. The angle between these two vectors is the phase difference between the voltage and the current. The phase difference is related to the time difference between the voltage and current. For example, a phase difference of
Formula used: V=
i =
Complete step by step answer:
In an AC circuit, the current and the voltage are an oscillating function (sinusoidal functions) of time. For example V=
In an AC circuit, we consider the voltage and the current as vectors. The angle between these is the phase difference between the voltage and the current in the circuit. The phase difference tells us how much the current is lagging behind or is ahead of the voltage.
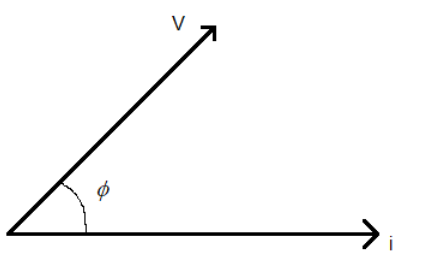
A phase difference of
We can relate the phase difference with the time difference between the current and the voltage. We know that a phase difference of
Therefore, a phase difference of
We know that
Therefore, the time difference between the voltage and the current is equal to
Hence, the correct option is (D).
Note: It is to be noted that the magnitudes of the vectors of the voltage and the current are the maximum values of the oscillating voltage and oscillating the current in an AC circuit, respectively.
Formula used: V=
i =
Complete step by step answer:
In an AC circuit, the current and the voltage are an oscillating function (sinusoidal functions) of time. For example V=
In an AC circuit, we consider the voltage and the current as vectors. The angle between these is the phase difference between the voltage and the current in the circuit. The phase difference tells us how much the current is lagging behind or is ahead of the voltage.

A phase difference of
We can relate the phase difference with the time difference between the current and the voltage. We know that a phase difference of
Therefore, a phase difference of
We know that
Therefore, the time difference between the voltage and the current is equal to
Hence, the correct option is (D).
Note: It is to be noted that the magnitudes of the vectors of the voltage and the current are the maximum values of the oscillating voltage and oscillating the current in an AC circuit, respectively.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

What are the major means of transport Explain each class 12 social science CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE




