
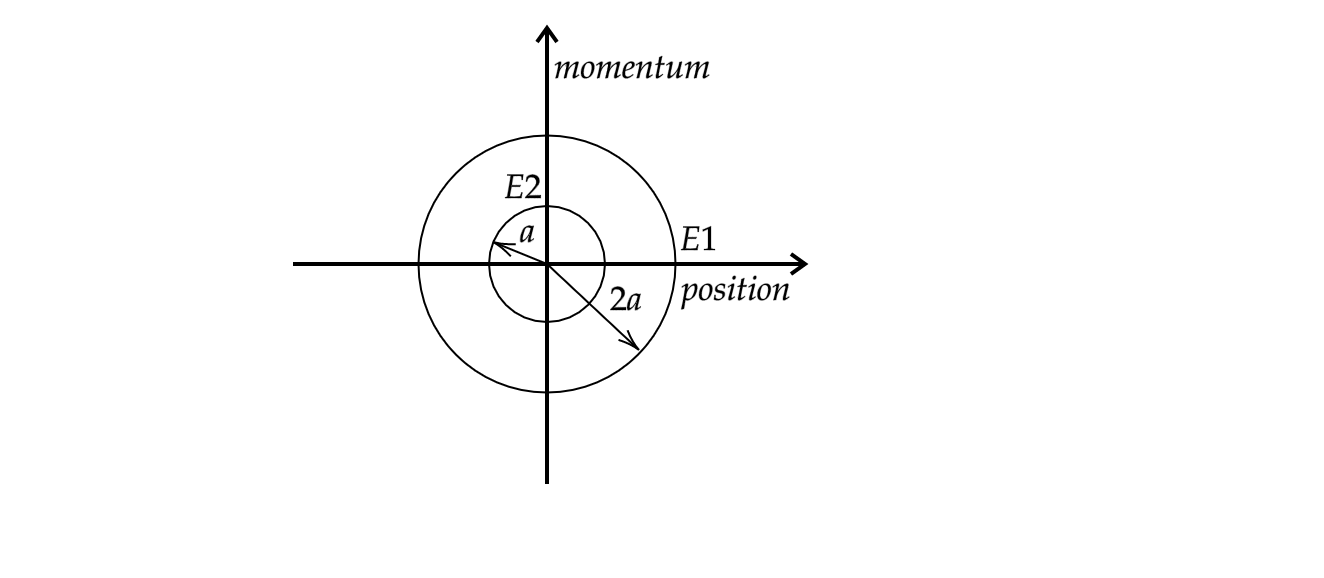
The phase space diagram for simple Momentum harmonic motion is a circle centred at the origin. In the figure, the two circles represent the same oscillator but for different initial conditions, and \[{{E}_{1}}\] ,\[{{E}_{2}}\] are the total mechanical energies respectively. Then:
(A) \[{{E}_{1}}=\sqrt{2}{{E}_{2}}\]
(B) \[{{E}_{1}}=2{{E}_{2}}\]
(C) \[{{E}_{1}}=4{{E}_{2}}\]
(D) \[{{E}_{1}}=16{{E}_{2}}\]
Answer
232.8k+ views
Hint: The diagram given to us is the phasor diagram for the simple harmonic motion of the oscillator. The radius of the circle gives us the amplitude of oscillations of the oscillator and the angular velocity for the circle gives us the frequency of oscillation of the oscillator. We need to find the mechanical energy of the oscillator in the two cases.
Formula Used:
$\implies$ \[K=\dfrac{1}{2}m{{v}^{2}}\]
$\implies$ \[P=m\times v\]
$\implies$ \[K=\dfrac{{{P}^{2}}}{2m}\]
Complete step by step answer:
In case of simple harmonic motion, at the mean position of oscillation, the total mechanical energy appears in the form of kinetic energy and at the extreme positions, the total mechanical energy appears in the form of potential energy. Hence, the total mechanical energy of the oscillator is equal to the kinetic energy in the mean position.
The mean position of the oscillator is shown by the y-axis in the given figure. Since the momentum of the two cases is marked along the y-axis, we can say that \[{{P}_{1}}=2{{P}_{2}}\] where \[P\] denotes momentum of the oscillator.
From the equations \[K=\dfrac{1}{2}m{{v}^{2}}\] and \[P=m\times v\] , we can say that \[K=\dfrac{{{P}^{2}}}{2m}\] where \[P\] denotes momentum and \[K\] denotes kinetic energy of the particle in oscillation
Now, substituting the values of momentum for the two cases, we have
\[{{E}_{1}}=\dfrac{{{(2{{P}_{1}})}^{2}}}{2m}\] and \[{{E}_{2}}=\dfrac{{{P}_{1}}^{2}}{2m}\] where \[{{E}_{1}}\] and \[{{E}_{2}}\] are the total mechanical energies of the oscillations
Taking the ratio of the two energies obtained, we get
\[\dfrac{{{E}_{1}}}{{{E}_{2}}}=\dfrac{4}{1}\Rightarrow {{E}_{1}}=4{{E}_{2}}\]
Hence option (C) is the correct answer.
Note: We can alternatively solve this question with the help of the relation of kinetic energy in simple harmonic motion and the amplitude of the oscillation, that is \[K=\dfrac{1}{2}m{{\omega }^{2}}{{A}^{2}}\] where \[K\] is the kinetic energy, \[\omega \] is the frequency of oscillation and \[A\] is the amplitude of oscillation. If we approach the question using this method, we won’t even need the diagram. We can just use the statement that their amplitudes are in the ratio \[2:1\] .
Formula Used:
$\implies$ \[K=\dfrac{1}{2}m{{v}^{2}}\]
$\implies$ \[P=m\times v\]
$\implies$ \[K=\dfrac{{{P}^{2}}}{2m}\]
Complete step by step answer:
In case of simple harmonic motion, at the mean position of oscillation, the total mechanical energy appears in the form of kinetic energy and at the extreme positions, the total mechanical energy appears in the form of potential energy. Hence, the total mechanical energy of the oscillator is equal to the kinetic energy in the mean position.
The mean position of the oscillator is shown by the y-axis in the given figure. Since the momentum of the two cases is marked along the y-axis, we can say that \[{{P}_{1}}=2{{P}_{2}}\] where \[P\] denotes momentum of the oscillator.
From the equations \[K=\dfrac{1}{2}m{{v}^{2}}\] and \[P=m\times v\] , we can say that \[K=\dfrac{{{P}^{2}}}{2m}\] where \[P\] denotes momentum and \[K\] denotes kinetic energy of the particle in oscillation
Now, substituting the values of momentum for the two cases, we have
\[{{E}_{1}}=\dfrac{{{(2{{P}_{1}})}^{2}}}{2m}\] and \[{{E}_{2}}=\dfrac{{{P}_{1}}^{2}}{2m}\] where \[{{E}_{1}}\] and \[{{E}_{2}}\] are the total mechanical energies of the oscillations
Taking the ratio of the two energies obtained, we get
\[\dfrac{{{E}_{1}}}{{{E}_{2}}}=\dfrac{4}{1}\Rightarrow {{E}_{1}}=4{{E}_{2}}\]
Hence option (C) is the correct answer.
Note: We can alternatively solve this question with the help of the relation of kinetic energy in simple harmonic motion and the amplitude of the oscillation, that is \[K=\dfrac{1}{2}m{{\omega }^{2}}{{A}^{2}}\] where \[K\] is the kinetic energy, \[\omega \] is the frequency of oscillation and \[A\] is the amplitude of oscillation. If we approach the question using this method, we won’t even need the diagram. We can just use the statement that their amplitudes are in the ratio \[2:1\] .
Recently Updated Pages
JEE Main 2023 April 6 Shift 1 Question Paper with Answer Key

JEE Main 2023 April 6 Shift 2 Question Paper with Answer Key

JEE Main 2023 (January 31 Evening Shift) Question Paper with Solutions [PDF]

JEE Main 2023 January 30 Shift 2 Question Paper with Answer Key

JEE Main 2023 January 25 Shift 1 Question Paper with Answer Key

JEE Main 2023 January 24 Shift 2 Question Paper with Answer Key

Trending doubts
JEE Main 2026: Session 2 Registration Open, City Intimation Slip, Exam Dates, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

Understanding the Angle of Deviation in a Prism

Hybridisation in Chemistry – Concept, Types & Applications

How to Convert a Galvanometer into an Ammeter or Voltmeter

Understanding Uniform Acceleration in Physics

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Laws of Motion Class 11 Physics Chapter 4 CBSE Notes - 2025-26

Waves Class 11 Physics Chapter 14 CBSE Notes - 2025-26

Mechanical Properties of Fluids Class 11 Physics Chapter 9 CBSE Notes - 2025-26

Thermodynamics Class 11 Physics Chapter 11 CBSE Notes - 2025-26

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26




