Question

The position vectors of the points A and B with respect to O are 2i+2j+k and 2i+4j+4k. The length of the internal bisector of
A.\[\sqrt {\dfrac{{136}}{9}} \]
B. \[\sqrt {\dfrac{{136}}{3}} \]
C. \[\dfrac{{20}}{3}\]
D. \[\sqrt {\dfrac{{217}}{9}} \]
E. \[\dfrac{{25}}{3}\]

Answer 1

Hint: If a is any position vector, then the magnitude of that vector can be determined by using formula. Also we can find the point that divides any line by section formula.

Formula used:
Let a be any position vector,
\[a = {a_1}i + {b_1}j + {c_1}k\]
\[\left| {\overrightarrow a } \right| = \sqrt {{a_1}^2 + {b_1}^2 + {c_1}^2} \]
Where i is unit vector along x-axis, j is unit vector along y-axis and z is unit vector along z-axis.
\[\left| {\overrightarrow a } \right|\] is the magnitude of position vector \[\overrightarrow a \]
If P is the point that divides the line \[({x_1},{y_1})\,{\rm{ and }}\,({x_2},{y_2}){\rm{ }}\], then section formula ,
\[\begin{array}{l}P(x,y) = (\dfrac{{m{x_2}{\rm{ + n}}{{\rm{x}}_1}}}{{m + n}},\dfrac{{m{y_2}{\rm{ + n}}{{\rm{y}}_1}}}{{m + n}})\\\end{array}\]
Where m and n are defined the division of the line segment into a ratio m:n.

Complete step by step solution:

Image: side AB divided in ratio 2:1
Position vector of OA and OB is given, we find the magnitude
\[\overrightarrow {OA} = 2i + 2j + k\]
\[\begin{array}{l}\left| {\overrightarrow {OA} } \right| = \sqrt {{2^2} + {2^2} + {1^2}} \\ \Rightarrow \left| {\overrightarrow {OA} } \right|{\rm{ = }}\sqrt {4 + 4 + 1} \\ \Rightarrow \left| {\overrightarrow {OA} } \right|{\rm{ = }}\sqrt 9 \\{\rm{ = 3}}\end{array}\]
Also, \[\overrightarrow {OB} = 2i + 4j + 4k\]
\[\begin{array}{l}\left| {\overrightarrow {OB} } \right| = \sqrt {{2^2} + {4^2} + {4^2}} \\ \Rightarrow \left| {\overrightarrow {OB} } \right|{\rm{ = }}\sqrt {4 + 16 + 16} \\ \Rightarrow \left| {\overrightarrow {OB} } \right|{\rm{ = }}\sqrt {36} \\ \Rightarrow \left| {\overrightarrow {OB} } \right|{\rm{ = 6}}\end{array}\]

The length OD(in figure) of the internal bisector of divided the line AB as m:n =2:1by angle bisector rule,

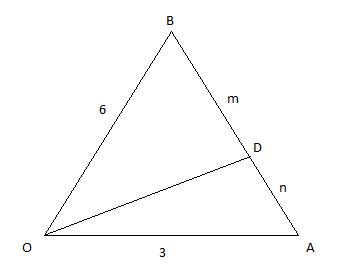
Image: side AB divided in ratio 2:1

As, \[{\rm{ }}\dfrac{m}{n} = \dfrac{{OA}}{{OB}} = \dfrac{3}{6} = \dfrac{1}{2}\]
By section formula,
\[\begin{array}{l}\overrightarrow {OD} = \dfrac{{m \times \overrightarrow {OB} {\rm{ + n}} \times \overrightarrow {OA} }}{{m + n}}\\\end{array}\]
Substituting the values, we get
\[\overrightarrow {OD} = 2i + \dfrac{8}{3}j + 2k\]
Magnitude of this position vector is
\[\begin{array}{l}\left| {\overrightarrow {OD} } \right| = \sqrt {{2^2} + {{\dfrac{8}{3}}^2} + {2^2}} \\ \Rightarrow \left| {\overrightarrow {OD} } \right|{\rm{ = }}\sqrt {4 + \dfrac{{64}}{9} + 4} \\ \therefore \left| {\overrightarrow {OD} } \right|{\rm{ = }}\sqrt {\dfrac{{136}}{9}} \\\end{array}\]
Therefore the length of internal bisector OD is \[\sqrt {\dfrac{{136}}{9}}\].

Hence, option A is the correct answer.

Note:In kinematics, the position vector specifies the position of a body. It gives the position or the location of any given point with respect to any reference point like origin in general. The change in the position vector of a body is known as the displacement vector. It is also defined as the vector distance between the initial point and the final point.