Question

The power dissipated across resistor ${R_5}$ in the network given below is

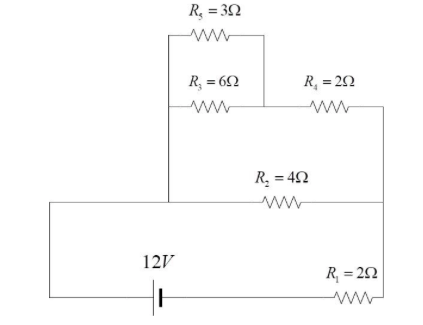
A. 3 watt B. $\dfrac{3}{4}$ watt
C. $\dfrac{{27}}{4}$ watt D. 9 watt

Answer 1

Hint:In order to find power through a resistor, the required quantities are current through the resistor and the resistance of the resistor. By these, the power can be calculated by the Joule’s law of heating –
$P = {I^2}R$
where I = current and R = resistance.
Step-by-step solution:
When 2 resistors are connected in series, the net resistance of the combination is the sum of the individual resistances.
$R = {R_1} + {R_2}$
When 2 resistors are connected in parallel, the net resistance of the combination is the reciprocal of the sum of reciprocals of individual resistances.
$\dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}$
$ \Rightarrow R = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}$
Consider the arrangement of resistors connected in the given fashion, subject to the potential difference of 12V.

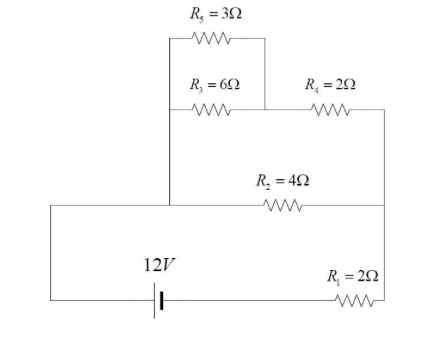
In this circuit, the resistors are connected as follows:
The parallel combination of ${R_3}$ is connected to ${R_5}$. This combination is in series with ${R_4}$. This entire combination is in parallel with ${R_2}$. The above entire combination is in series with ${R_1}$.
Hence, the net resistance R is given by –
$R = {R_1} + \left( {{R_2}//\left( {\left( {{R_3}//{R_5}} \right) + {R_4}} \right)} \right)$
Let us substitute the values one-by-one and determine the resistance by applying the above formula for the net resistance.
${R_3}//{R_5} = \dfrac{{{R_3}{R_5}}}{{{R_3} + {R_5}}} = \dfrac{{3 \times 6}}{{3 + 6}} = \dfrac{{18}}{9} = 2\Omega $
${R_3}//{R_5} + {R_4} = 2 + 2 = 4\Omega $
${R_2}//\left( {\left( {{R_3}//{R_5}} \right) + {R_4}} \right) = 4//4 = \dfrac{{4 \times 4}}{{4 + 4}} = \dfrac{{16}}{8} = 2\Omega $
Finally, the net resistance is the series combination of ${R_1}$ with the above combination.
$R = {R_1} + 2 = 2 + 2 = 4\Omega $
The net current is given by –
$I = \dfrac{V}{R} = \dfrac{{12}}{4} = 3A$
In a parallel combination, the current branches depending on the resistances in the branches.
The current flowing through the combination ${R_2}//\left( {\left( {{R_3}//{R_5}} \right) + {R_4}} \right)$ and ${R_1}$ is the same since they are in series.
The current branches in the parallel combination of ${R_2}$ and ${R_3}//{R_5} + {R_4}$ .
The branch current is calculated by the formula, ${I_1} = \dfrac{{I{R_2}}}{{{R_1} + {R_2}}}$
Applying the branch current formula to the combination of ${R_3}//{R_5} + {R_4}$, we have –
${I_{{R_3}//{R_5} + {R_4}}} = {I_{C3}} = \dfrac{{I{R_2}}}{{\left( {{R_3}//{R_5} + {R_4}} \right) + {R_2}}} = \dfrac{{3 \times 4}}{{4 + 4}} = \dfrac{{12}}{8} = \dfrac{3}{2}A$
Now, the current ${I_{C3}}$ flowing through the parallel combination ${R_3}//{R_5}$ and ${R_4}$ is the same since they are in series. This current branches in the parallel combination.
The branch current, \[{I_5} = \dfrac{{{I_{C3}}{R_3}}}{{{R_3} + {R_4}}} = \dfrac{{\dfrac{3}{2} \times 6}}{{6 + 3}} = \dfrac{9}{9} = 1A\]
Hence, the power across ${R_5}$ ,
$P = I_5^2{R_5} = {1^2} \times 3 = 1 \times 3 = 3W$

Hence, the correct option is Option A.

Note:The formula for derivation of branch current is as follows:
If ${R_1}$ and ${R_2}$ are in parallel, the current through resistor ${R_1}$ , is given by –
${I_1} = \dfrac{V}{{{R_1}}}$
where V = potential difference across the combination.
The potential difference across the combination is given by –
$V = I{R_p}$
where I = current in main branch and ${R_p}$ = net resistance of combination
${R_p} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}$
Substituting,
$V = I\dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}$
Thus,
${I_1} = \dfrac{V}{{{R_1}}}$
${I_1} = \dfrac{I}{{{R_1}}} \times \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} = \dfrac{{I{R_2}}}{{{R_1} + {R_2}}}$