Question

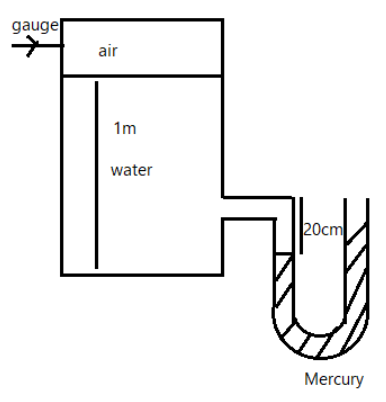
The pressure gauge reading in meter of water column shown in the given figure will be:

\[\begin{align}
  & A.3.20m \\
 & B.2.72m \\
 & C.2.52m \\
 & D.1.52m \\
\end{align}\]

Answer 1

Hint: We know that a fluid exerts pressure on the surface. Here the pressure due to the water is equal to the pressure due to the mercury. The pressure head is given due to the height of the water. Thus we need to calculate the height of the water.
Formula: $P=h\rho g$

Complete answer:
Since fluid exerts pressure on the surroundings. We also know that pressure is defined as the force per unit area. Then the pressure of the fluid column is proportional to the height of the column. Then, $P\propto h$
From fluid pressure, we know that the pressure is given as $P=h\rho g$ where $\rho$ is the density of the fluid and $g$ is the acceleration due to the gravity and $h$is the height of the column.
Let us assume that there is no loss of pressure. Since the pressure due to the water exerts a pressure on the mercury column completely, we can say that $p_{w}=p_{m}$
Let us consider the u-tube which is filled with mercury. Given that the $h_{m}=20cm=0.2m$ we know that the density of mercury $\rho_{m}=13546kg/m^{3}$ and the density of the water $\rho_{w}=997kg/m^{3}$.
Then substituting the values, we get, $h_{w}\rho_{w}g=h_{m}\rho_{m}g$
$\implies h_{w}=h_{m}\dfrac{\rho_{m}}{\rho_{w}}$
Substituting the value, $h_{w}=0.2\times\dfrac{13546}{997}=2.717=2.72m$
Thus the pressure head in the column is given as $2.72\;m$

Hence the answer is option \[B.2.72m\] .

Note:
Pressure gauge or pressure meter is used to measure the pressure exerted by the fluid. Here, we are calculating the differential pressure between the tubes, where the difference in the height is measured using the pressure gauge. This is the value we are trying to calculate here.