Question

The probability that a student will pass the final examination in both English and Hindi is 0.5 and the probability of passing neither is 0.1. If the probability of passing the English examination is 0.75. what is the probability of passing the Hindi examination?

Answer 1

Hint: From the Venn diagram, we will form an equation as the sum of all probability is equal to 1, after getting the equation, we will find the probability of passing the Hindi examination that will be the only unknown factor in the equation.

Complete step by step answer:

Given data:
${\text{P(E}} \cap {\text{H) = 0}}{\text{.5}}$
${\text{P[(E}} \cup {\text{H)'] = 0}}{\text{.1}}$
${\text{P(E) = 0}}{\text{.75}}$
$(A \cup B)'$denotes the area neither containing A nor B.

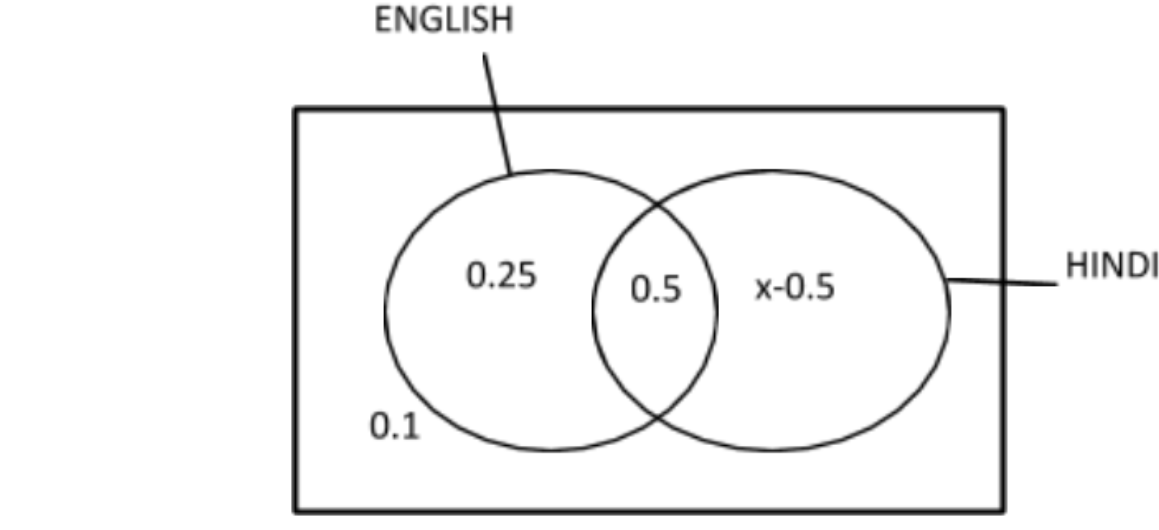
Now, we know that ${\text{A}} \cap {\text{B}}$ is used for the area that is falling under both A and B, and A-B is known for that area that contained A but not B so we can say that
$ \Rightarrow {\text{P(E) - P(E}} \cap {\text{H) = 0}}{\text{.75 - 0}}{\text{.5}}$
${\text{ = 0}}{\text{.25}}$
Let us assume that${\text{P(H) = x}}$
We know that the sum of all the probability of any event is 1.
Therefore, we can write as
${\text{P(E) + P(H) - P(E}} \cap {\text{H) + P[(E}} \cup {\text{H)'] = 1}}$
Because ${\text{P(E}} \cap {\text{H)}}$is in both probability i.e. ${\text{P(E)}}$and ${\text{P(H)}}$, subtracting once
$ \Rightarrow {\text{0}}{\text{.75 + x - 0}}{\text{.5 + 0}}{\text{.1 = 1}}$
$ \Rightarrow {\text{x = 1 - 0}}{\text{.75 + 0}}{\text{.5 - 0}}{\text{.1}}$
$ \Rightarrow {\text{x = 1}}{\text{.5 - 0}}{\text{.85}}$
$ \Rightarrow {\text{x = 0}}{\text{.65}}$
$\therefore {\text{P(H) = 0}}{\text{.65}}$
Hence, the probability of passing the Hindi Examination is \[0.65\]

Note: The probability of any event is always greater than equal to 0 and lesser or equal to 1. If the probability of an event is 0 it is known as an impossible event and if the probability of an event is 1 then it is certain that event will happen.