Question

The quadrilateral which has both line and rotational symmetry of order more than $2$ is
A. Rectangle
B. Rhombus
C. Square
D. Parallelogram

Answer 1

Hint: First we have to know about the line symmetry and rotational symmetry in quadrilaterals. Then, one by one we will discuss about the properties of rectangle, rhombus, square and parallelogram. So, we get a clear idea about all this shapes and it helps us to choose a correct answer.

Complete step by step answer:
As we know that the quadrilateral is a two dimensional shape with four sides. Now let us discuss the line symmetry and rotational symmetry. Line symmetry is a mirror image taking place across a line. Rotational symmetry is that a shape rotated around a point.
Now, let us start with a rectangle-
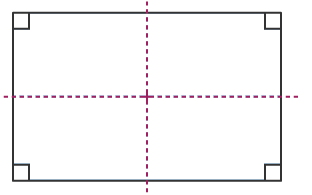
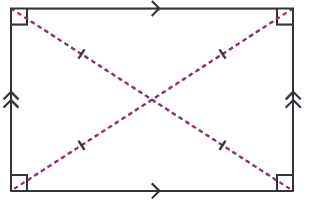
As we know that a rectangle is a quadrilateral in which opposite sides are equal and parallel. A rectangle has four right angles. Diagonals bisect each other. A rectangle has two lines of symmetry and also has rotational symmetry of order two.

Now, a rhombus-
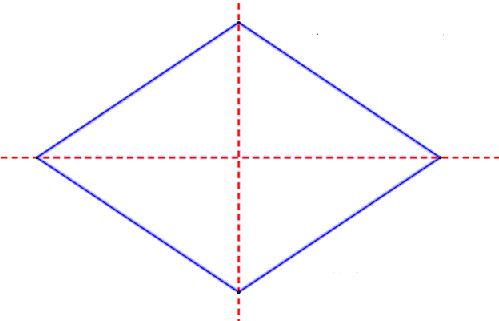
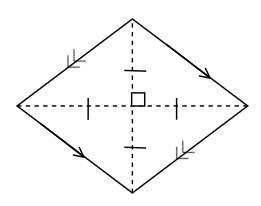
A rhombus has all sides equal and opposite angles equal. Diagonals of a rhombus bisect each other at right angles. A rhombus has two lines of symmetry and has rotational symmetry of order two.

Now, square-
As we know that a square has four sides equal and has four right angles. The diagonals bisect each other at right angles. A square has four lines of symmetry and has rotational symmetry of order four.

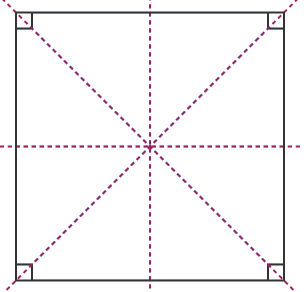
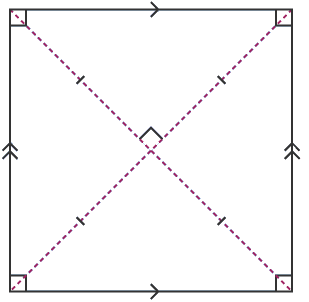
Also we know that parallelograms have opposite sides equal and parallel. Parallelogram has no line of symmetry but has rotational symmetry of order two.

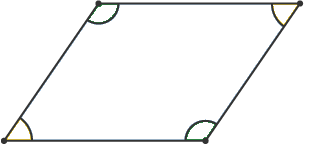
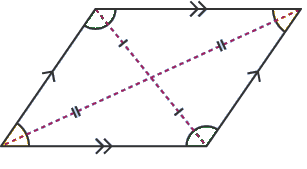
So, when we recall the properties of these entire quadrilaterals we get the solution.

So, the correct answer is “Option C”.

Note: Before solving this question a student must have a clear idea about line symmetry and rotational symmetry. Also recall the properties of these quadrilaterals.