Question

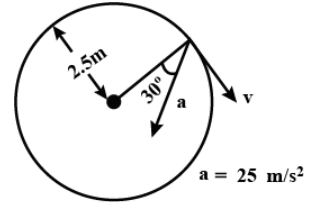
The radial acceleration is

A.$1.65m{s}^{-2}$
B.$5.65m{s}^{-2}$
C.$11.65m{s}^{-2}$
D.$21.65m{s}^{-2}$

Answer 1

Hint: We have to find radial or centripetal acceleration here.
We need to break the acceleration vector into its two rectangular components.
As we know, centripetal acceleration is always along the centre and radius in a circle.so the horizontal component of the given acceleration vector will be the radial acceleration of the body .Also, radial acceleration is always perpendicular to the velocity vector.

Complete answer:
Centripetal acceleration is responsible for a body’s moment in circular motion.it is the acceleration due to the force which is resultant of all the forces acting on the body.
The radial or centripetal acceleration is perpendicular to the velocity vector.
As the angle between radius vector and net acceleration is given, we will break the given acceleration into its vertical and horizontal components and we will see that the horizontal component is the radial or centripetal acceleration as it is along the centre and radius of the circular path.
It a vector $\overrightarrow{c}$ makes an angle $\theta$ with the horizontal then its rectangular components will be,
Horizontal component -$c\cos \theta$
Vertical component-$c\sin \theta$.

So according to above information, the components of acceleration will be
Horizontal component -$a\cos {30}^o$
Vertical component-$a\sin {30}^o$.
Given value,
a=$25ms{}^{-2}$
Radial acceleration:
$\Rightarrow 25\times \cos {30}^o$
$\Rightarrow 25\times 0.866$
$\Rightarrow 21.65m{s}^{-2}$

Hence the radial acceleration has come and the correct option is D.

Note:
The perpendicular component of the acceleration $a\sin {30}^o$is known as tangential acceleration.it is directed in or opposite to the direction of velocity.
It is responsible for change in the magnitude of velocity.
Also, it is present only in the case of non-uniform circular motion.