
The radius of gyration of a uniform disc about a line perpendicular to the disc equals its radius. Find the distance of the line from the centre.
Answer
488.7k+ views
Hint:The given line is mentioned to be perpendicular to the disc. As the radius of gyration equals the radius of the disc, the required distance can be obtained using the parallel axis theorem. The parallel axis theorem gives the moment of inertia of the disc about the given line as the sum of the moment of inertia of the disc about an axis passing through its centre of mass and parallel to the given line and the product of its mass and the square of the required distance.
Formulas used:
-The moment of inertia of a disc about a perpendicular axis passing through its centre is given by,
-The moment of inertia of a body is given by,
Complete step by step answer.
Step 1: Sketch a figure representing the given line perpendicular to the disc and list the parameters of the given disc.
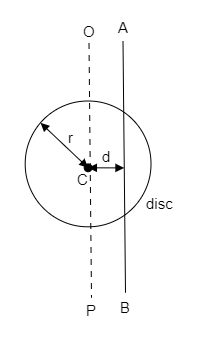
In the above figure, C represents the centre of the disc. AB is the line perpendicular to the disc at a distance
The radius of the disc is denoted by
Let
Let
The moment of inertia about the axis OP which is perpendicular to the disc and passing through the centre is known to be
Step 2: Express the moment of inertia of the disc about the axis AB using the parallel axis theorem.
The moment of inertia of the disc about the axis AB is usually expressed in terms of the radius of gyration as
Since
We can also express the moment of inertia about AB based on the parallel axis theorem as
Substituting equations (1) and (2) in (3) we get,
Cancelling
Thus the distance from the centre to the axis AB is
Note:The radius of gyration is a geometric property of a body. It also depends on the position and configuration of the axis of rotation of the body. The centre of mass of the body is independent of the axis of rotation and it is fixed as the body rotates. However, the radius of gyration will change in response to the variations in the axis of rotation.
Formulas used:
-The moment of inertia of a disc about a perpendicular axis passing through its centre is given by,
-The moment of inertia of a body is given by,
Complete step by step answer.
Step 1: Sketch a figure representing the given line perpendicular to the disc and list the parameters of the given disc.

In the above figure, C represents the centre of the disc. AB is the line perpendicular to the disc at a distance
The radius of the disc is denoted by
Let
Let
The moment of inertia about the axis OP which is perpendicular to the disc and passing through the centre is known to be
Step 2: Express the moment of inertia of the disc about the axis AB using the parallel axis theorem.
The moment of inertia of the disc about the axis AB is usually expressed in terms of the radius of gyration as
Since
We can also express the moment of inertia about AB based on the parallel axis theorem as
Substituting equations (1) and (2) in (3) we get,
Cancelling
Thus the distance from the centre to the axis AB is
Note:The radius of gyration is a geometric property of a body. It also depends on the position and configuration of the axis of rotation of the body. The centre of mass of the body is independent of the axis of rotation and it is fixed as the body rotates. However, the radius of gyration will change in response to the variations in the axis of rotation.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Master Class 12 Economics: Engaging Questions & Answers for Success

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Write a short note on Franklands reaction class 12 chemistry CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

What are the major means of transport Explain each class 12 social science CBSE




