Question

The radius of the circle is 13 cm and the length of one of its chords is 10 cm, find the distance of the chord from the center.

Answer 1

Hint: First look at the definition of the chord of a circle. By this try to draw a random chord of length given (10 cm). Now drop a perpendicular from the center on to chord. Try and prove that this perpendicular will bisect the cord. So by this, you get a right-angle triangle. Assume the length of perpendicular as l. Apply Pythagoras theorem to find the value of l. This value of l will be the distance of the chord from the center which is the required result.

Complete step-by-step solution -
Chord: A line segment whose both the endpoints lie on the circle is called a chord.
Let us take an example of a chord in a circle with center O and radius r.

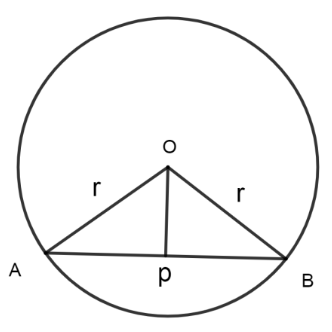
Here as AB is a chord, we know that points A, B lie on the circle. So, we get that OA, OB is the radius. As the circle radius is r, we say $OA = OB = r$.
As two sides are equal, we say that the triangle OAB is an isosceles triangle.
By general properties of the isosceles triangle, we know that the perpendicular from a vertex will bisect the side opposite to that vertex.
So, if AB is the chord of length x then the distance AP will be $\dfrac{x}{2}$.
In our case let us take the diagram with chord length 10 cm. And the length of perpendicular to be l. By or assumption, we have the values as:
$AB = \,10\,cm\,\,,\,\,OA = radius = 13\,cm\,\,,\,\,OP = l$

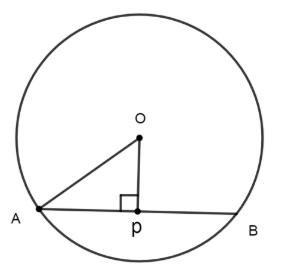
Radius is given to be 13cm, for the given circle. By our proof before, we can say that P bisects the line AB. By this we can say value of AP to be as:
$AP = \dfrac{{AB}}{2} = \dfrac{{10}}{2} = 5\,cm$
As we can see that the triangle OAP is right angled triangle. We can apply Pythagoras theorem to this triangle. We can establish a relation between sides, we get it as:
$O{A^2} = A{P^2} + O{P^2}$
By substituting all the values as you know, we get it as:
${13^2} = {5^2} + O{P^2}$
By subtracting with ${5^2}$ on both sides and simplify, we get:
$O{P^2} = {13^2} - {5^2} = 169 - 125 = 144$
By applying square root on both sides, we get:
$OP = \sqrt {144} = 12\,cm$
Therefore the distance of the chord from the center is 12 cm.

Note: The proof of perpendicular from the center to the chord bisects it is very important. Because it is the base point of the whole solution. While taking square root do not consider the negative root as OP denotes the distance of length. Length can never be negative. The perpendicular length is itself distance we require.