
The range of the ammeter is 5 amperes, and the full-scale deflection current is 0.5 micro-amperes. If the resistance of the galvanometer is 50 ohms, then find the shunt resistance.
Answer
497.7k+ views
Hint: In this question, we need to determine the value of the shunt resistance that should be attached in parallel with the 50 ohms resistance such that the full-scale deflection of the ammeter is 0.5 micro-amperes whereas the total range of the ammeter is 5 Amperes. For this, we will use the relations for Kirchhoff’s law.
Complete step by step answer:The internal resistance of the ammeter is connected in series, and to extend the range of the ammeter, an additional resistance should be connected in parallel with the internal resistance. The resistances connected in parallel are known as Shunt resistances.
Here, the full-scale deflection is
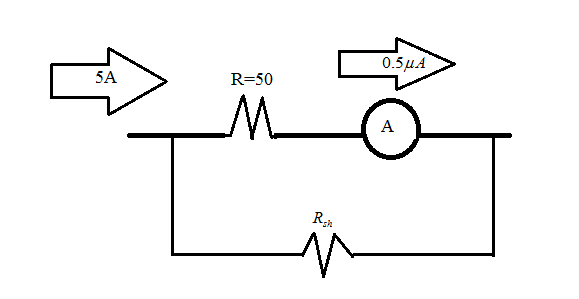
As we know, the potential drop across the resistances connected in parallel is the same. SO,
Hence, the value of the shunt resistance that should be connected in parallel with the ammeter is 5 micro-ohms.
Note:It is interesting to note here that as we need to increase the range of the ammeter so we have connected a very low value of the resistance so that a major part of the current inline will flow through it without harming the meter.
Complete step by step answer:The internal resistance of the ammeter is connected in series, and to extend the range of the ammeter, an additional resistance should be connected in parallel with the internal resistance. The resistances connected in parallel are known as Shunt resistances.
Here, the full-scale deflection is

As we know, the potential drop across the resistances connected in parallel is the same. SO,
Hence, the value of the shunt resistance that should be connected in parallel with the ammeter is 5 micro-ohms.
Note:It is interesting to note here that as we need to increase the range of the ammeter so we have connected a very low value of the resistance so that a major part of the current inline will flow through it without harming the meter.
Latest Vedantu courses for you
Grade 7 | CBSE | SCHOOL | English
Vedantu 7 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹42,330 per year
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Trending doubts
Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Which one of the following is a true fish A Jellyfish class 12 biology CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Write the difference between solid liquid and gas class 12 chemistry CBSE




