
The ratio of its rotational kinetic energy and translational kinetic energy of a sphere, which is rolling without slipping on a horizontal plane, will be:
(A) $5:2$
(B) $2:5$
(C) $7:5$
(D) $5:7$
Answer
216.6k+ views
Hint The kinetic energy of the body is the sum of its rotational kinetic energy and the translational kinetic energy about the center of mass of the rigid sphere. Here the center of mass is at the point $O$. Also, it has been given that there is no slip, i.e. the relative velocity of the point $A$ on both the sphere and the ground $0$. Therefore we have $v = \omega R$.
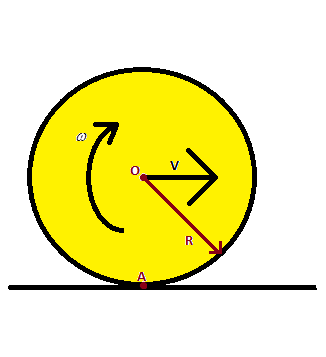
Complete Step by step solution We will separately calculate the rotational kinetic energy and translational kinetic energy and find their ratios. The rotational energy of any body is given by $\dfrac{1}{2}I{\omega ^2}$, where $I$ is the mass moment of inertia, and $\omega $ is the angular velocity about the center of mass of the body $O$.
This energy will vary with different objects as for various objects, the moment of inertia $I$ will vary.
For this solid sphere, $K.E{._{rotational}} = \dfrac{1}{2}I{\omega ^2} = \dfrac{1}{2}(\dfrac{2}{5}M{r^2}){\omega ^2}$
Therefore, substituting $v = \omega R$ in $K.E{._{rotational}} = \dfrac{1}{2}I{\omega ^2} = \dfrac{1}{2}(\dfrac{2}{5}M{r^2}){\omega ^2}$, we get
$ \Rightarrow K.E{._{rotational}} = \dfrac{1}{2}(\dfrac{2}{5}M{r^2}){(\dfrac{v}{r})^2}$,
$ \Rightarrow K.E{._{rotational}} = \dfrac{1}{5}M{v^2}$, where $v$ is the translational velocity at the center of mass of the body $O$.
Now we will find the translational kinetic energy of the solid sphere.
Translational kinetic energy is given by $K.E{._{translational}} = \dfrac{1}{2}M{v^2}$
Now the ratio of the rotational kinetic energy to the translational kinetic energy is, $\dfrac{{K.E{._{rotational}}}}{{K.E{._{translational}}}} = \dfrac{{\dfrac{1}{5}M{v^2}}}{{\dfrac{1}{2}M{v^2}}} = \dfrac{2}{5}$
Hence the correct answer is an option (B).
Note Here we consider the sphere as a solid body. If the sphere would have been hollow, then the moment of inertia would be $\dfrac{{2M{R^2}}}{3}$, in which case the answer would be $\dfrac{{K.E{._{rotational}}}}{{K.E{._{translational}}}} = \dfrac{{\dfrac{1}{3}M{v^2}}}{{\dfrac{1}{2}M{v^2}}} = \dfrac{2}{3}$. The velocity at the contact between the ground and the sphere is $0$ and at the top, most point of the sphere is $v + R\omega $, which is equal to $2v$ , and is the fastest moving point on the sphere.

Complete Step by step solution We will separately calculate the rotational kinetic energy and translational kinetic energy and find their ratios. The rotational energy of any body is given by $\dfrac{1}{2}I{\omega ^2}$, where $I$ is the mass moment of inertia, and $\omega $ is the angular velocity about the center of mass of the body $O$.
This energy will vary with different objects as for various objects, the moment of inertia $I$ will vary.
For this solid sphere, $K.E{._{rotational}} = \dfrac{1}{2}I{\omega ^2} = \dfrac{1}{2}(\dfrac{2}{5}M{r^2}){\omega ^2}$
Therefore, substituting $v = \omega R$ in $K.E{._{rotational}} = \dfrac{1}{2}I{\omega ^2} = \dfrac{1}{2}(\dfrac{2}{5}M{r^2}){\omega ^2}$, we get
$ \Rightarrow K.E{._{rotational}} = \dfrac{1}{2}(\dfrac{2}{5}M{r^2}){(\dfrac{v}{r})^2}$,
$ \Rightarrow K.E{._{rotational}} = \dfrac{1}{5}M{v^2}$, where $v$ is the translational velocity at the center of mass of the body $O$.
Now we will find the translational kinetic energy of the solid sphere.
Translational kinetic energy is given by $K.E{._{translational}} = \dfrac{1}{2}M{v^2}$
Now the ratio of the rotational kinetic energy to the translational kinetic energy is, $\dfrac{{K.E{._{rotational}}}}{{K.E{._{translational}}}} = \dfrac{{\dfrac{1}{5}M{v^2}}}{{\dfrac{1}{2}M{v^2}}} = \dfrac{2}{5}$
Hence the correct answer is an option (B).
Note Here we consider the sphere as a solid body. If the sphere would have been hollow, then the moment of inertia would be $\dfrac{{2M{R^2}}}{3}$, in which case the answer would be $\dfrac{{K.E{._{rotational}}}}{{K.E{._{translational}}}} = \dfrac{{\dfrac{1}{3}M{v^2}}}{{\dfrac{1}{2}M{v^2}}} = \dfrac{2}{3}$. The velocity at the contact between the ground and the sphere is $0$ and at the top, most point of the sphere is $v + R\omega $, which is equal to $2v$ , and is the fastest moving point on the sphere.
Recently Updated Pages
JEE Atomic Structure and Chemical Bonding important Concepts and Tips

JEE Amino Acids and Peptides Important Concepts and Tips for Exam Preparation

Electricity and Magnetism Explained: Key Concepts & Applications

Chemical Properties of Hydrogen - Important Concepts for JEE Exam Preparation

JEE Energetics Important Concepts and Tips for Exam Preparation

JEE Isolation, Preparation and Properties of Non-metals Important Concepts and Tips for Exam Preparation

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

Understanding Collisions: Types and Examples for Students

How to Convert a Galvanometer into an Ammeter or Voltmeter

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26

NCERT Solutions For Class 11 Physics Chapter 8 Mechanical Properties Of Solids

Motion in a Straight Line Class 11 Physics Chapter 2 CBSE Notes - 2025-26

NCERT Solutions for Class 11 Physics Chapter 7 Gravitation 2025-26

Understanding Atomic Structure for Beginners




