Question

The rear side of a truck is open and a box of mass $2kg$ is placed on the truck $8m$ away from the open end. The truck starts from rest with an acceleration of $2ms^{-2}$ on a straight road. The box will fall off the truck when it is at a distance from the starting point equal to (Given $\mu = 0.1$ and $g = 10 ms^{-2}$):
A. 4m
B. 8m
C. 12m
D.16m

Answer 1

Hint: You might find it useful to first calculate the time it takes for the box to fall off the truck and then use that to obtain the distance the truck would have travelled in that time. Do not forget that the box is placed on the accelerating truck which could influence the net acceleration of the box.

Formula used: Equation of motion for distance travelled by an accelerating body from rest
$$ S = ut +\dfrac{1}{2}at^2 \Rightarrow S = \dfrac{1}{2}at^2 $$
Since $u=0 ms^{-1}$ for a body starting from rest.
Force acting on a body of mass m accelerating at a $ms^{-2}$
$$F = ma$$
Limiting force acting on a body as a result of a frictional force (with coefficient of friction $\mu$) of mass m accelerating at a $ms^{-2}$ while being subjected to normal reaction:
$$F = \mu N= \mu mg$$

Complete step by step answer:
Let us deconstruct the problem for a better understanding of the influencing forces on the box.
We have a truck that has a box on its trailer and it starts from rest. This means that the initial velocity of both the truck and the box is $u = 0 ms^{-1}$.

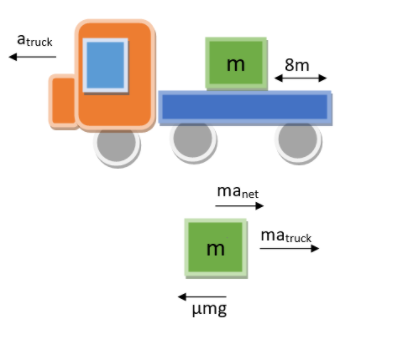
The truck is accelerating ($a_{truck}\;ms^{-2}$) on a straight road, i.e., the box is also under the influence of this acceleration. So the force acting on the box due to the acceleration of the truck is a pseudo force, i.e.,
$$F_{pseudo force} = ma_{truck} = 2 \times 2 = 4 kg m s^{-2}$$
However, there is also a limiting (frictional) force acting on the box, so,
$$F_{limiting} = \mu mg = 0.1 \times 2 \times 10 = 2 kg m s^{-2}$$
The net force acting on the box can be written as:
$$F_{net} = ma_{net}$$
This is basically the difference between the contributing pseudo force and limiting force,i.e.,
$$F_{net} = F_{pseudo force} - F_{limiting} = 4 – 2 = 2 kg m s^{-2}$$
$$\Rightarrow ma_{net} = 2 kg m s^{-2} \Rightarrow a_{net} = \dfrac{2 kg m s^{-2}}{2 kg} = 1 ms^{-2} $$
Now that we’ve obtained the net acceleration of the box, we can use the following kinetic equation of motion to determine the time it takes for the box to travel $S=8m$:
$$ S = ut +\dfrac{1}{2}at^2 \Rightarrow S = \dfrac{1}{2}at^2 $$
$$\Rightarrow t = \sqrt{\dfrac{2S}{a_{net}}} = \sqrt{\dfrac{2 \times 8}{1}} = 4 seconds $$
We can now apply the same equation of motion to determine the distance the truck would have travelled just as the box will fall of at 4s, i.e.,
$$ S = \dfrac{1}{2}at^2 = \dfrac{1}{2} \times 2 \times 4^2 = 16m $$

So, the correct answer is “Option D”.

Note: It is important to remember to include the frictional force as it contributed to impeding the motion of the box, without which our calculation would yield a completely different but an incorrect result.
It is also necessary to deconstruct the scenario to isolate the forces acting on both the truck and the box and to determine which are the final contributing forces that influence the distance the truck travels. It always helps to sketch out the scenario in developing a more efficient approach to dealing with problems with cross-influencing forces.