Question

The rectangular solid is to be cut into two rectangular solids. Answer the following based on the conditions indicated in columns A and B.
Column A: The total surface area of the two resulting pieces if the cut is made through point P.
Column B: The total surface area of the two resulting pieces if the cut is made through point Q.

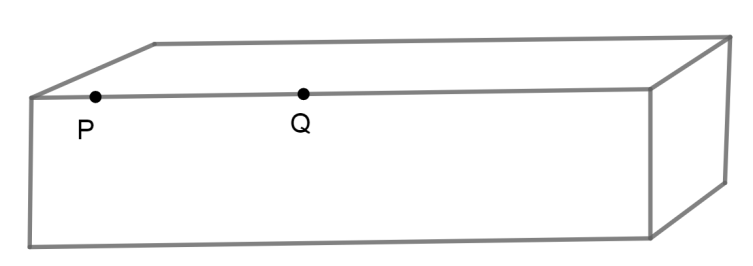
A. The quantity in Column A is greater.
B. The quantity in Column B is greater.
C. The two quantities are equal.
D. The relationship cannot be determined from the information given.

Answer 1

Hint: Assume length of piece cut before as x. Similarly assume breadth height correspondingly. Now find the total surface of 2 parts separately. Now the results of both the surface area. By this you get a relation between total surface area and new length x. By this you can compare the cuts at two different points.

Complete step by step solution:
Given in the question, about the solid figure is written as:
The rectangular solid is cut into two rectangular solids.

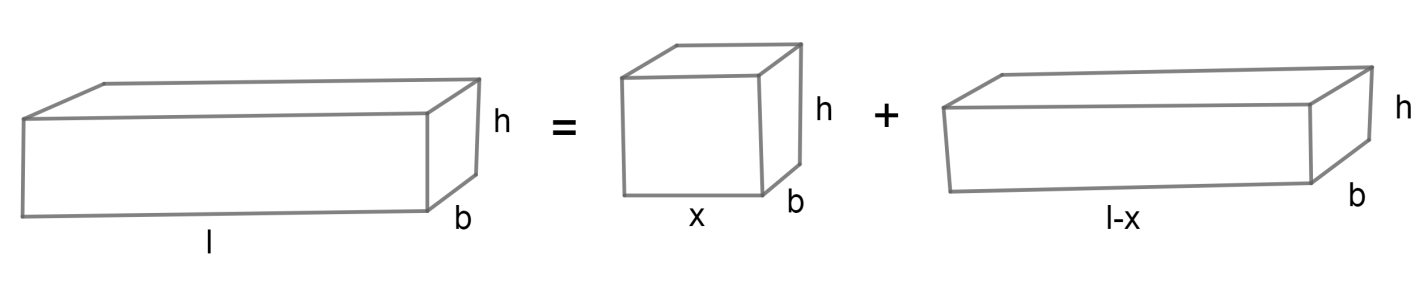
Let us assume the length of the original solid is l.
And let us assume the first piece has length of x. Then the length of the second piece will be l-x.
Let us assume the breadth of original solid is b.
Then we get the first piece has the same breadth of b. And by symmetry we get the breadth of the second piece is also b. Because cut is parallel to breadth. Perpendicular to the length of the solid. Let us assume the height of the original solid is denoted by h. Then we get the second piece has the same height of h. By symmetry we get the height of the second piece is also h. Because the cut is parallel to height. Whereas perpendicular to length of solid. Total surface area is defined as the sum of areas of all surfaces of the solid.
Now areas of opposite surfaces are equal. So, if we find area of 3 surfaces and multiply by 2, we get total area.
Area of a rectangle with side lengths as a,b cab be:
Area = $a\text{ }\times \text{ b}$
By using this to surface b, x in first piece, we get it as:
${{A}_{1}}\text{ = bx}$
By using this to surface h, x in first piece, we get it as:
${{A}_{2}}\text{ = hx}$
By using this to surface h, b in first piece, we get it as:
${{A}_{3}}\text{ = hb}$
By using this to surface of second piece, we get them as:
${{A}_{4}}\text{ = }\left( \text{l-x} \right)\text{ b, }{{\text{A}}_{\text{5}}}\text{ = }\left( \text{l-x} \right)\text{ b, }{{\text{A}}_{\text{6}}}\text{ = hb}$
Using this to original surface, we get them as follows:
${{A}_{7}}\text{ = lb }{{\text{A}}_{\text{8}}}\text{ = bh }{{\text{A}}_{\text{9}}}\text{ = hl}$
Total surface area of first piece $=\text{ 2}\left( {{A}_{1}}+{{A}_{2}}+{{A}_{3}} \right)$
Total surface area of second piece $=\text{ 2}\left( {{A}_{4}}+{{A}_{5}}+{{A}_{6}} \right)$
Total after cutting is sum of both areas above $=\text{ 2}\left( {{A}_{1}}+{{A}_{2}}+{{A}_{3}}+{{A}_{4}}+{{A}_{5}}+{{A}_{6}} \right)$
By substituting them, we get it as $=\text{ 2}\left( bx+hx+bh+\left( l-x \right)b+\left( l-x \right)h+bh \right)$
By simplifying we cancel x terms as opposite sign $=\text{ 2}\left( lb+2bh+lh \right)$
By adding $2\left( {{A}_{7}},{{A}_{8}},{{A}_{9}} \right)$we get total surface of original. By substituting original $=\text{ 2}\left( lb+2bh+lh \right)$
If we cut through P the value of x is unknown so let it be x.
Let the area formed by cutting through P is A.
By the above equation, we get it as:
$A=\text{ 2}\left( lb+2bh+lh \right)$
If we cut through Q the value of x is \[\dfrac{length}{2}\].
By substituting this however it cancels with itself.
Let the area formed by cutting through Q is B.
By the above equation, we get it as:
$B=\text{ 2}\left( lb+2bh+lh \right)$
Both are equal. So, the position of the cut does not matter; total surface areas are always the same if the cut is perpendicular to length.
Therefore, option (c) is the correct answer.

Note: Be careful you must observe breadth, height remains same. Generally students forget and assume they change by other variables then you cannot solve the question. You must carefully observe what you are changing.