Question

What should be the refracting angle of a prism of refractive index 1.5 in order that the ray incident on the face at an angle of 50° may suffer minimum deviation?

Answer 1

Hint: This problem can be solved using Snell's law. Snell’s law describes the relation between angle of refraction and angle of incidence. Substitute the values in Snell’s law and obtain the value for angle of refraction. Angle of minimum deviation is twice the angle of refraction. So. Multiply the obtained value for angle of refraction by 2. This obtained value will be the refracting angle of the prism to suffer minimum deviation.

Complete answer:

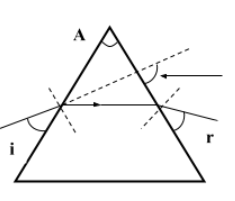
Given: Incident angle (i)= 50°
Refractive index of prism ($\mu$)= 1.5
Snell’s law is given by,
$\mu = \dfrac {\sin {i}} {\sin {r}}$
Substituting the given values in above equation we get,
$\Rightarrow 1.5 =\dfrac {\sin {50}} {\sin {r}}$
$\Rightarrow \sin {r} = \dfrac {\sin {i}}{1.5}$
$\Rightarrow \sin {r} = \dfrac {0.766}{1.5}$
$\Rightarrow \sin {r}= 0.510$
$\Rightarrow r= {\sin}^{-1}{(0.510)}$
$\Rightarrow r= 30.66°$
Now, the angle of minimum deviation is twice the angle of refraction.
$\therefore {\delta}_{m} = 2r$
Substituting the values in above equation we get,
${\delta}_{m} = 2 \times 30.66°$
$\Rightarrow {\delta}_{m} = 61.32°$

Hence, the refracting angle of the prism for minimum deviation should be 61.32°.

Note:
There are few conditions which are satisfied for minimum deviation through the prism. The conditions are as follows:
1.The angle of emergence should be equal to the angle of incident.
2.The ray passing through the prism should be parallel to the base of the prism.
3.The incident ray should be refracted parallel to the side opposite to the angle of the prism.
If the minimum deviation is equal to the refracting angle then the angle of prism and refraction angles will also be equal.