Question

The refractive indices of the crown glass for blue and red light are \[1.51\] and \[1.49\] respectively, and those of the flint glass are \[1.77\] and \[1.73\], respectively. An isosceles prism of angle $6^{\circ}$ is made of crown glass. A beam of white light is incident at a small angle on this prism. The other flint glass isosceles prism is combined with the crown glass prism such that there is no deviation of the incident light. If net dispersion of the combined system is $\dfrac{x}{100}$. Find $x$.

Answer 1

Hint: To calculate the net dispersion, calculate the dispersion due to each prism, by taking the average of the refractive indices. Since there is no deviation, we can equate the deviation of the combination to $0$.

Formula used:
$\delta=\delta_{c}+\delta_{f}$
$\delta=(\mu-1)A$

Complete step by step answer:
Given that, for crown glass,
Refractive index for blue light: $\mu_{b}=1.51$
Refractive index for red light: $\mu_{r}=1.49.$
Angle $A_{c}=6^{\circ}$
For flint,
Refractive index for blue light: $\mu_{b}\prime=1.77$
Refractive index for red light: $\mu_{r}\prime=1.73$
Angle $A_{f}=x$
For combination of prisms, net deviation is given by $\delta=\delta_{c}+\delta_{f}$, where $\delta_{c}$ is the deviation due to crown prism and $\delta_{f}$ is the deviation due to flint prism.

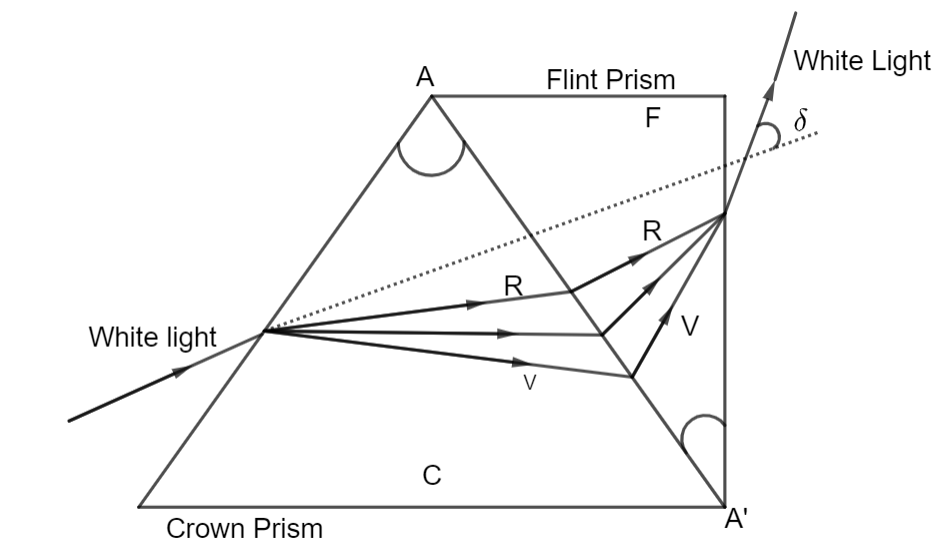
For no deviation $\delta=\delta_{c}+\delta_{f}=0$
$\delta_{c}=-\delta_{f}$
We also know that $\delta=(\mu-1)A$ where $\mu$ is the average refractive index
Then, $\mu=\dfrac{\mu_{b}+\mu_{r}}{2}=\dfrac{1.51+1.49}{2}=1.50$
Similarly, $\mu\prime=\dfrac{\mu_{b}\prime+\mu_{r}\prime}{2}=\dfrac{1.77+1.73}{2}=1.75$
Then from $\delta_{c}=-\delta_{f}$
$(\mu-1)A_{c}=-(\mu\prime-1)A_{f}$
$(1.50-1)\times 6=-(1.75-1)\times x$
$x=-\dfrac{0.5\times 6}{0.75}$
$x=-4^{\circ}$
Hence, the net dispersion angle of the flint is $4^{\circ}$.

Note:
The negative sign implies that the combination must be another way. i.e. the flint followed by the crown prism. Only since there is no deviation, we equate the net deviation to $0$, which reduces the problem to a simple ratio.